12. CHAPTER 12. FURTHER TOPICS IN MULTIPLE REGRESSION#
SET UP
library(foreign) # to open stata.dta files
library(psych) # for better sammary of descriptive statistics
library(repr) # to combine graphs with adjustable plot dimensions
options(repr.plot.width = 12, repr.plot.height = 6) # Plot dimensions (in inches)
options(width = 150) # To increase character width of printed output
12.1. Load Libraries (Packages)#
Show code cell source
pkgs <- c("car", "lmtest", "sandwich","tseries","forecast","bayesreg","psych")
invisible(lapply(pkgs, function(pkg) suppressPackageStartupMessages(library(pkg, character.only = TRUE))))
12.2. 12.1 Inference with Robust Standard Errors#
12.2.1. Load and summarize data#
df <- read.dta("Dataset/AED_HOUSE.DTA")
df_desc<-describe(df)
print(df_desc)
vars n mean sd median trimmed mad min max range skew kurtosis se
price 1 29 253910.34 37390.71 244000 249296.00 22239.00 204000 375000 171000 1.48 2.23 6943.28
size 2 29 1882.76 398.27 1800 1836.00 296.52 1400 3300 1900 1.64 3.29 73.96
bedrooms 3 29 3.79 0.68 4 3.72 0.00 3 6 3 0.92 1.89 0.13
bathrooms 4 29 2.21 0.34 2 2.16 0.00 2 3 1 1.28 0.23 0.06
lotsize 5 29 2.14 0.69 2 2.16 0.00 1 3 2 -0.17 -1.00 0.13
age 6 29 36.41 7.12 35 36.20 5.93 23 51 28 0.44 -0.75 1.32
monthsold 7 29 5.97 1.68 6 6.04 1.48 3 8 5 -0.47 -1.03 0.31
list 8 29 257824.14 40860.26 245000 252364.00 23721.60 199900 386000 186100 1.65 2.70 7587.56
12.2.2. Robust SE regression (Table 12.2)#
model <- lm(price ~ size + bedrooms + bathrooms + lotsize + age + monthsold, data = df)
coeftest(model, vcov = vcovHC(model, type = "HC1"))
t test of coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 137791.066 65545.225 2.1022 0.0472030 *
size 68.369 15.359 4.4514 0.0002003 ***
bedrooms 2685.315 8285.528 0.3241 0.7489257
bathrooms 6832.880 19283.791 0.3543 0.7264632
lotsize 2303.221 5328.860 0.4322 0.6697909
age -833.039 762.930 -1.0919 0.2866932
monthsold -2088.504 3738.270 -0.5587 0.5820214
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
12.2.3. HAC SE for mean#
df2 <- read.dta("Dataset/AED_REALGDPPC.dta")
print(describe(df2$growth))
model2 <- lm(growth ~ 1, data = df2) # mean regression
coeftest(model2, vcov = NeweyWest(model2, lag = 0)) # HAC with lag 0
coeftest(model2, vcov = NeweyWest(model2, lag = 5)) # HAC with lag 5
vars n mean sd median trimmed mad min max range skew kurtosis se
X1 1 241 1.99 2.18 2.09 2.08 1.8 -4.77 7.63 12.4 -0.38 0.64 0.14
t test of coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.99046 0.53261 3.7372 0.0002326 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
t test of coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.99046 0.65908 3.02 0.002801 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
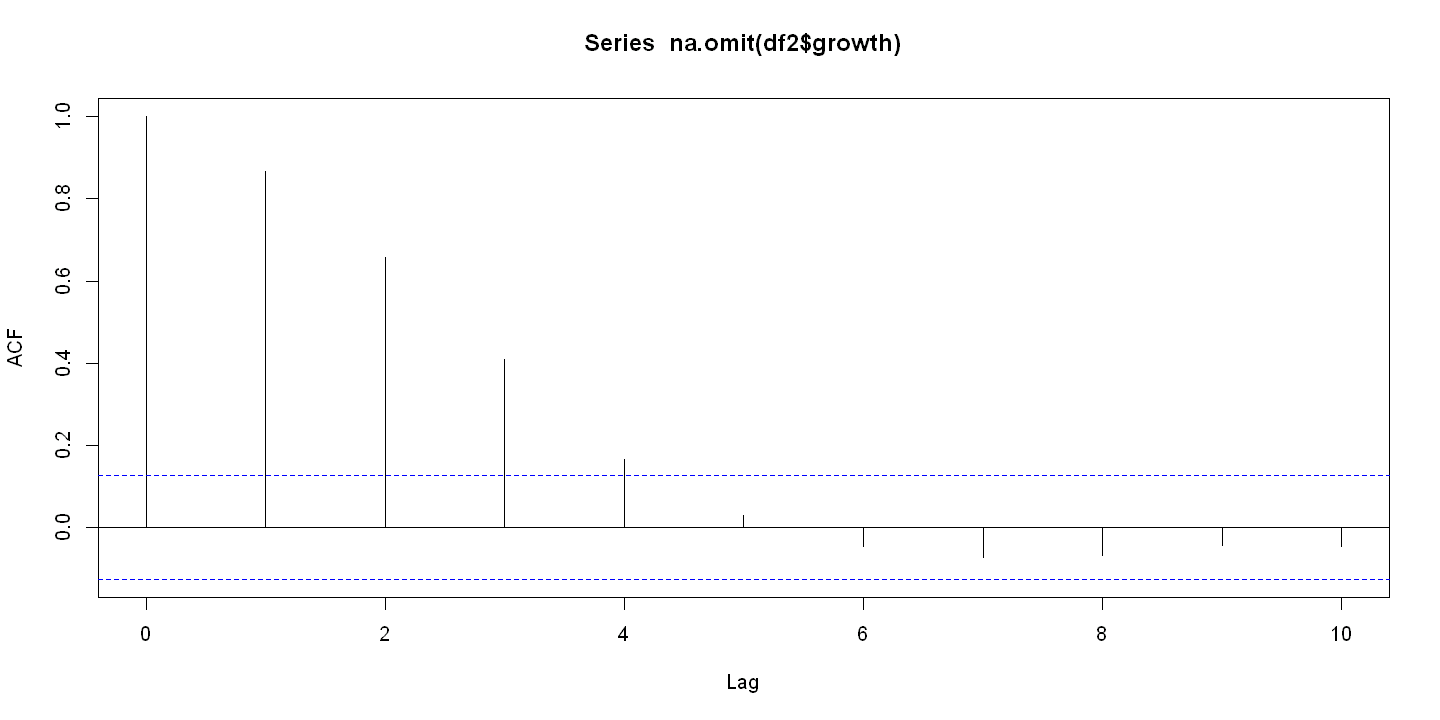
Lag manually
df2$growthlag1 <- dplyr::lag(df2$growth, 1)
cor(df2$growth, df2$growthlag1, use = "complete.obs")
0.868101170631149
Autocorrelation
12.3. 12.2 Prediction#
# Basic regression and CI at `size = 2000`
model_simple <- lm(price ~ size, data = df)
# Predict conditional mean at size = 2000
predict(model_simple, newdata = data.frame(size = 2000), interval = "confidence")
| fit | lwr | upr | |
|---|---|---|---|
| 1 | 262559.4 | 253192.2 | 271926.6 |
# Predict actual value at size = 2000
predict(model_simple, newdata = data.frame(size = 2000), interval = "prediction")
| fit | lwr | upr | |
|---|---|---|---|
| 1 | 262559.4 | 213337.9 | 311780.9 |
12.3.1. Confidence intervals manually#
xbar <- mean(df$size)
n <- nrow(df)
var_x <- var(df$size)
model <- lm(price ~ size, data = df)
b <- coef(model)
se <- summary(model)$sigma
y_cm <- b[1] + b[2]*2000
s_y_cm <- se * sqrt(1/n + (2000 - xbar)^2 / ((n - 1)*var_x))
s_y_f <- se * sqrt(1 + 1/n + (2000 - xbar)^2 / ((n - 1)*var_x))
tcrit <- qt(0.975, df = n - 2)
cat("Conditional mean CI: (", y_cm - tcrit*s_y_cm, ",", y_cm + tcrit*s_y_cm, ")\n")
cat("Prediction CI: (", y_cm - tcrit*s_y_f, ",", y_cm + tcrit*s_y_f, ")\n")
Conditional mean CI: ( 253192.2 , 271926.6 )
Prediction CI: ( 213337.9 , 311780.9 )
12.3.2. Multiple regression + CI#
model_full <- lm(price ~ size + bedrooms + bathrooms + lotsize + age + monthsold, data = df)
# Predict value for specified inputs
newdata <- data.frame(size = 2000, bedrooms = 4, bathrooms = 2, lotsize = 2, age = 40, monthsold = 6)
predict(model_full, newdata = newdata, interval = "confidence")
predict(model_full, newdata = newdata, interval = "prediction")
# Define values for predictors
new_x <- c(1, 2000, 4, 2, 2, 40, 6) # intercept + values for size, bedrooms, etc.
# Extract coefficients and covariance matrix
beta_hat <- coef(model_full)
vcov_mat <- vcov(model_full)
# Compute point estimate (ŷ)
y_hat <- sum(new_x * beta_hat)
# Compute standard error using delta method
se_hat <- sqrt(t(new_x) %*% vcov_mat %*% new_x)
# Compute confidence interval (95%)
t_crit <- qt(0.975, df = df.residual(model_full))
ci_lower <- y_hat - t_crit * se_hat
ci_upper <- y_hat + t_crit * se_hat
# Display result
cat(sprintf("Prediction: %.2f\n", y_hat))
cat(sprintf("95%% CI: (%.2f, %.2f)\n", ci_lower, ci_upper))
| fit | lwr | upr | |
|---|---|---|---|
| 1 | 257690.8 | 244235 | 271146.6 |
| fit | lwr | upr | |
|---|---|---|---|
| 1 | 257690.8 | 204255.3 | 311126.3 |
Prediction: 257690.80
95% CI: (244234.97, 271146.63)
12.3.3. Robust SE with lincom#
Robust SE
coeftest(model_full, vcov = vcovHC(model_full, type = "HC1"))
t test of coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 137791.066 65545.225 2.1022 0.0472030 *
size 68.369 15.359 4.4514 0.0002003 ***
bedrooms 2685.315 8285.528 0.3241 0.7489257
bathrooms 6832.880 19283.791 0.3543 0.7264632
lotsize 2303.221 5328.860 0.4322 0.6697909
age -833.039 762.930 -1.0919 0.2866932
monthsold -2088.504 3738.270 -0.5587 0.5820214
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
12.4. 12.8 Bayesian Methods (Overview)#
Bayesian Regression (Informative and non-informative priors)
df$pricenew <- df$price / 1000
set.seed(10101)
# Run Bayesian regression with a valid prior ("ridge")
model_bayes <- bayesreg(pricenew ~ size, data = df, model = "normal", prior = "ridge")
summary(model_bayes)
==========================================================================================
| Bayesian Penalised Regression Estimation ver. 1.3 |
| (c) Enes Makalic, Daniel F Schmidt. 2016-2024 |
==========================================================================================
Bayesian Gaussian ridge regression Number of obs = 29
Number of vars = 1
MCMC Samples = 1000 std(Error) = 24.993
MCMC Burnin = 1000 R-squared = 0.6159
MCMC Thinning = 5 WAIC = 134.46
-------------+-----------------------------------------------------------------------------
Parameter | mean(Coef) std(Coef) [95% Cred. Interval] tStat Rank ESS
-------------+-----------------------------------------------------------------------------
size | 0.07007 0.01253 0.04524 0.09465 5.591 1 ** 879
(Intercept) | 121.78160 24.01663 74.02427 170.98904 . . .
-------------+-----------------------------------------------------------------------------