9. CHAPTER 09. MODELS WITH NATURAL LOGARITHMS#
SET UP
library(foreign) # to open stata.dta files
library(psych) # for better sammary of descriptive statistics
library(repr) # to combine graphs with adjustable plot dimensions
options(repr.plot.width = 12, repr.plot.height = 6) # Plot dimensions (in inches)
options(width = 150) # To increase character width of printed output
9.1. 9.4 EXAMPLE: EARNINGS AND EDUCATION#
df = read.dta(file = "Dataset/AED_EARNINGS.DTA")
attach(df)
print(describe(df))
print(head(df))
vars n mean sd median trimmed mad min max range skew kurtosis se
earnings 1 171 41412.69 25527.05 36000 38052.70 17049.90 1050 172000 170950 1.70 4.23 1952.10
education 2 171 14.43 2.74 14 14.45 2.97 3 20 17 -0.45 1.16 0.21
age 3 171 30.00 0.00 30 30.00 0.00 30 30 0 NaN NaN 0.00
gender 4 171 0.00 0.00 0 0.00 0.00 0 0 0 NaN NaN 0.00
earnings education age gender
1 25000 14 30 0
2 40000 12 30 0
3 25000 13 30 0
4 38000 13 30 0
5 28800 12 30 0
6 31000 16 30 0
Create variables and add to data frame
lnearn = log(earnings)
df$lnearn = lnearn
lneduc = log(education)
df$lneduc = lneduc
9.1.1. Table 9.2#
table92vars = c("earnings", "lnearn", "education", "lneduc")
print(describe(df[table92vars]))
vars n mean sd median trimmed mad min max range skew kurtosis se
earnings 1 171 41412.69 25527.05 36000.00 38052.70 17049.90 1050.00 172000.00 170950.0 1.70 4.23 1952.10
lnearn 2 171 10.46 0.62 10.49 10.47 0.54 6.96 12.06 5.1 -0.90 4.74 0.05
education 3 171 14.43 2.74 14.00 14.45 2.97 3.00 20.00 17.0 -0.45 1.16 0.21
lneduc 4 171 2.65 0.22 2.64 2.66 0.20 1.10 3.00 1.9 -2.42 13.27 0.02
9.1.2. Table 9.3#
Linear model
ols.linear <- lm(earnings ~ education)
library(jtools)
summ(ols.linear, digits=3)
MODEL INFO:
Observations: 171
Dependent Variable: earnings
Type: OLS linear regression
MODEL FIT:
F(1,169) = 68.857, p = 0.000
R² = 0.289
Adj. R² = 0.285
Standard errors:OLS
----------------------------------------------------------
Est. S.E. t val. p
----------------- ------------ ---------- -------- -------
(Intercept) -31055.915 8887.835 -3.494 0.001
education 5021.123 605.101 8.298 0.000
----------------------------------------------------------
Log-linear Model
summ(ols.loglin <- lm(lnearn ~ education), digits=3)
MODEL INFO:
Observations: 171
Dependent Variable: lnearn
Type: OLS linear regression
MODEL FIT:
F(1,169) = 84.743, p = 0.000
R² = 0.334
Adj. R² = 0.330
Standard errors:OLS
--------------------------------------------------
Est. S.E. t val. p
----------------- ------- ------- -------- -------
(Intercept) 8.561 0.210 40.825 0.000
education 0.131 0.014 9.206 0.000
--------------------------------------------------
Log-log Model
summ(ols.loglog <- lm(lnearn ~ lneduc), digits=3)
MODEL INFO:
Observations: 171
Dependent Variable: lnearn
Type: OLS linear regression
MODEL FIT:
F(1,169) = 67.668, p = 0.000
R² = 0.286
Adj. R² = 0.282
Standard errors:OLS
--------------------------------------------------
Est. S.E. t val. p
----------------- ------- ------- -------- -------
(Intercept) 6.543 0.478 13.700 0.000
lneduc 1.478 0.180 8.226 0.000
--------------------------------------------------
Linear-log Model
summ(ols.linlog <- lm(earnings ~ lneduc), digits=3)
MODEL INFO:
Observations: 171
Dependent Variable: earnings
Type: OLS linear regression
MODEL FIT:
F(1,169) = 50.570, p = 0.000
R² = 0.230
Adj. R² = 0.226
Standard errors:OLS
------------------------------------------------------------
Est. S.E. t val. p
----------------- ------------- ----------- -------- -------
(Intercept) -102767.278 20347.617 -5.051 0.000
lneduc 54452.483 7657.259 7.111 0.000
------------------------------------------------------------
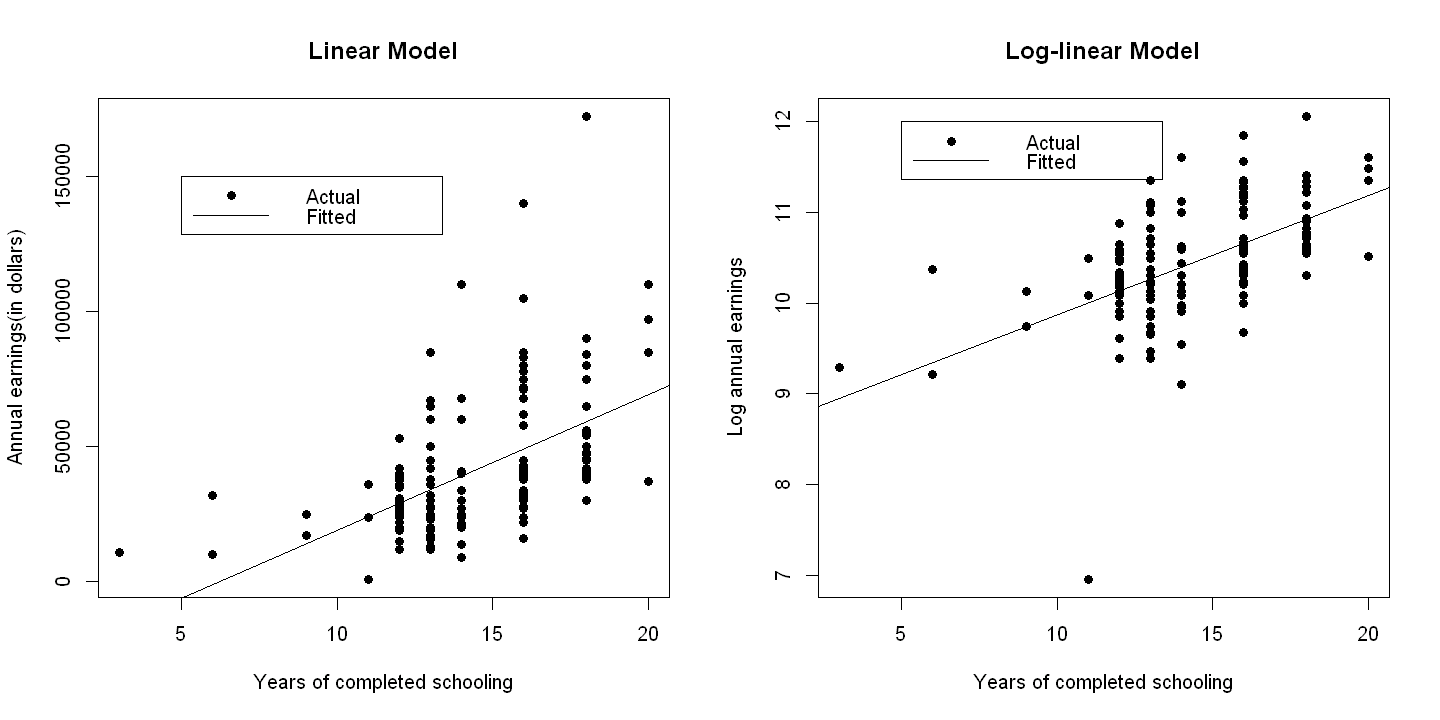
9.1.3. Figure 9.1#
par(mfrow = c(1,2))
# first panel
plot(education,earnings, xlab="Years of completed schooling",
ylab="Annual earnings(in dollars)",pch=19,main="Linear Model")
abline(ols.linear)
legend(5, 150000, c("Actual", "Fitted"), lty=c(-1,1), pch=c(19,-1), bty="o")
# second panel
plot(education,lnearn, xlab="Years of completed schooling",
ylab="Log annual earnings",pch=19,main="Log-linear Model")
abline(ols.loglin)
legend(5, 12, c("Actual", "Fitted"), lty=c(-1,1), pch=c(19,-1), bty="o")
9.2. 9.5 FURTHER USES OF THE NATURAL LOGARITHM#
9.2.1. Table 9.5#
rm(list=ls())
df = read.dta(file = "Dataset/AED_SP500INDEX.DTA")
attach(df)
print(describe(df))
print(head(df))
vars n mean sd median trimmed mad min max range skew kurtosis se
year 1 93 1973.00 26.99 1973.00 1973.00 34.10 1927.00 2019.00 92.00 0.00 -1.24 2.80
sp500 2 93 473.66 710.75 96.47 325.68 123.34 6.92 3230.78 3223.86 1.77 2.58 73.70
lnsp500 3 93 4.82 1.80 4.57 4.79 2.34 1.93 8.08 6.15 0.16 -1.27 0.19
year sp500 lnsp500
1 1927 17.66 2.871302
2 1928 24.35 3.192532
3 1929 21.45 3.065725
4 1930 15.34 2.730464
5 1931 8.12 2.094330
6 1932 6.92 1.934416
To predict exponential growth in the graph in levels
summ(ols.logs <- lm(lnsp500 ~ year))
plnsp500 = predict(ols.logs)
MODEL INFO:
Observations: 93
Dependent Variable: lnsp500
Type: OLS linear regression
MODEL FIT:
F(1,91) = 2070.52, p = 0.00
R² = 0.96
Adj. R² = 0.96
Standard errors:OLS
--------------------------------------------------
Est. S.E. t val. p
----------------- --------- ------ -------- ------
(Intercept) -124.09 2.83 -43.80 0.00
year 0.07 0.00 45.50 0.00
--------------------------------------------------
Correct for retransformation bias - see chapter 15.6. First need \(rmse^2\) the square of the root mean squared error. Code here uses knowledge that \(k = 2\)
ResSS = c(crossprod(ols.logs$residuals))
MSE = ResSS / (length(ols.logs$residuals) - 2)
sqrt(MSE)
psp500 = exp(plnsp500)*exp(MSE/2)
MSE
0.371732757916085
0.138185243307899
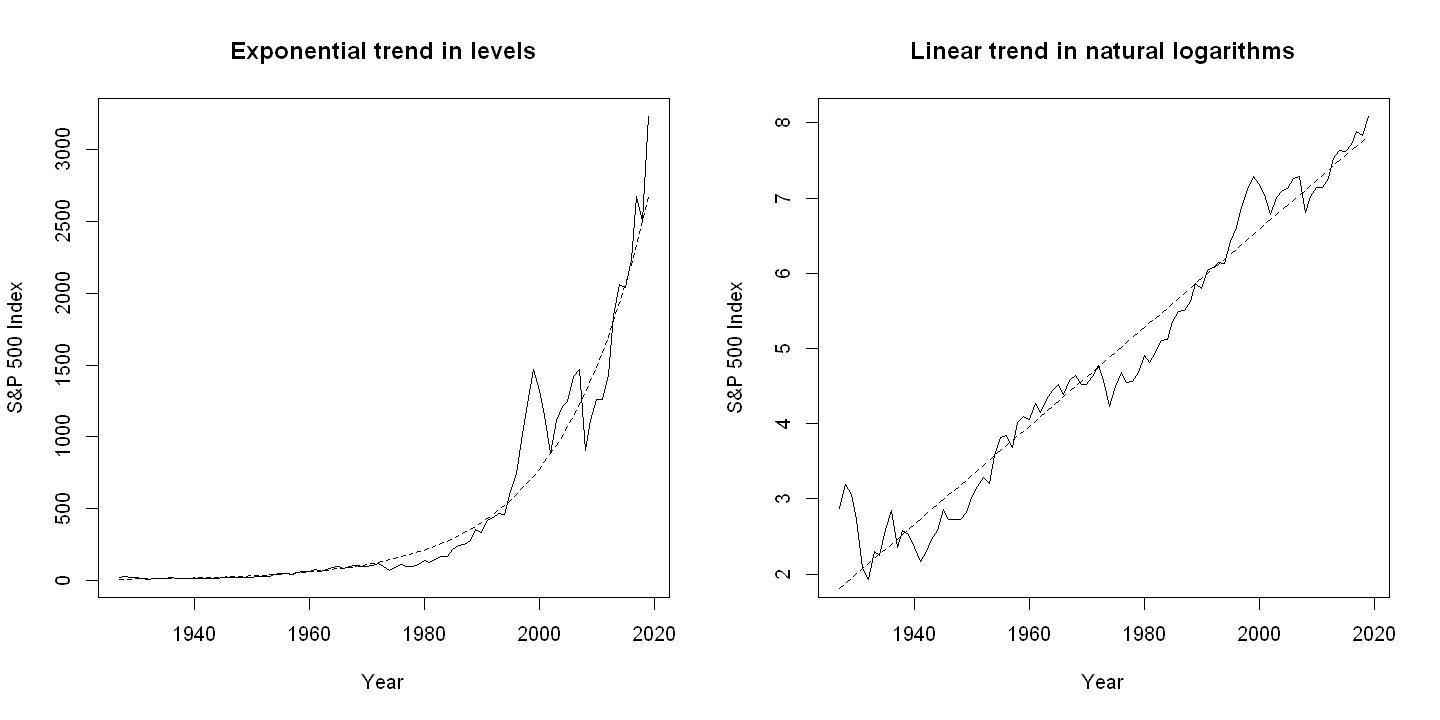
9.2.2. Figure 9.2#
par(mfrow = c(1,2))
# first panel
plot(year, sp500, xlab="Year", ylab="S&P 500 Index", type="l",lty=1,
main="Exponential trend in levels")
points(year, psp500, type="l",lty=2)
# second panel
plot(year, lnsp500, xlab="Year", ylab="S&P 500 Index", type="l",lty=1,
main="Linear trend in natural logarithms")
points(year, plnsp500, type="l",lty=2)