8. CHAPTER 8. CASE STUDIES FOR BIVARIATE REGRESSION#
SETUP
library(foreign) # to open stata.dta files
library(psych) # for better sammary of descriptive statistics
library(repr) # to combine graphs with adjustable plot dimensions
options(repr.plot.width = 12, repr.plot.height = 6) # Plot dimensions (in inches)
options(width = 150) # To increase character width of printed output
8.1. 8.1 HEALTH OUTCOMES ACROSS COUNTRIES#
# Read in the Stata data set - requires package foreignl
library(foreign)
df = read.dta(file = "Dataset/AED_HEALTH2009.DTA")
attach(df)
print(describe(df))
print(head(df))
vars n mean sd median trimmed mad min max range skew kurtosis se
country_name* 1 34 17.50 9.96 17.50 17.50 12.60 1.00 34.00 33.00 0.00 -1.31 1.71
year 2 34 2009.00 0.00 2009.00 2009.00 0.00 2009.00 2009.00 0.00 NaN NaN 0.00
hlthgdp 3 34 9.67 2.12 9.60 9.56 2.08 6.40 17.70 11.30 1.30 3.70 0.36
hlthpc 4 34 3255.65 1493.65 3188.50 3182.79 1600.47 923.00 7990.00 7067.00 0.67 0.96 256.16
infmort 5 34 4.45 2.72 3.70 3.89 1.04 1.80 14.70 12.90 2.49 6.12 0.47
lifeexp 6 34 76.70 2.94 77.65 77.06 2.08 69.80 79.90 10.10 -1.08 -0.07 0.50
gdppc 7 34 33054.04 12916.75 32899.48 32057.63 8976.71 13806.16 82900.88 69094.72 1.50 4.32 2215.20
code* 8 34 17.50 9.96 17.50 17.50 12.60 1.00 34.00 33.00 0.00 -1.31 1.71
hlthpcsq 9 34 12764623.35 11839147.56 10173338.50 11140525.46 8809621.80 851929.00 63840100.00 62988171.00 2.33 7.56 2030397.06
lnhlthpc 10 34 7.97 0.51 8.07 8.01 0.45 6.83 8.99 2.16 -0.58 -0.38 0.09
lngdppc 11 34 10.34 0.38 10.40 10.35 0.28 9.53 11.33 1.79 -0.16 0.30 0.06
lnlifeexp 12 34 4.34 0.04 4.35 4.34 0.03 4.25 4.38 0.14 -1.12 0.03 0.01
lninfmort 13 34 1.38 0.45 1.31 1.33 0.29 0.59 2.69 2.10 1.14 1.48 0.08
country_name year hlthgdp hlthpc infmort lifeexp gdppc code hlthpcsq lnhlthpc lngdppc lnlifeexp lninfmort
1 Australia 2009 9.1 3670 4.3 79.3 39039.96 AUS 13468900 8.207947 10.572341 4.373238 1.458615
2 Austria 2009 11.2 4346 3.8 77.6 38827.71 AUT 18887716 8.377011 10.566890 4.351567 1.335001
3 Belgium 2009 10.7 3911 3.4 77.3 36721.66 BEL 15295921 8.271548 10.511122 4.347694 1.223776
4 Canada 2009 11.4 4317 5.0 78.5 37842.29 CAN 18636488 8.370316 10.541183 4.363099 1.609438
5 Chile 2009 8.4 1210 7.9 75.8 15177.29 CHL 1464100 7.098376 9.627556 4.328098 2.066863
6 Czech Republic 2009 8.0 2048 2.9 74.2 25627.48 CZR 4194304 7.624619 10.151421 4.306764 1.064711
8.1.1. Table 8.1#
table81vars = c("hlthpc", "lifeexp", "infmort")
print(describe(df[table81vars]))
vars n mean sd median trimmed mad min max range skew kurtosis se
hlthpc 1 34 3255.65 1493.65 3188.50 3182.79 1600.47 923.0 7990.0 7067.0 0.67 0.96 256.16
lifeexp 2 34 76.70 2.94 77.65 77.06 2.08 69.8 79.9 10.1 -1.08 -0.07 0.50
infmort 3 34 4.45 2.72 3.70 3.89 1.04 1.8 14.7 12.9 2.49 6.12 0.47
Key regression
ols.lifeexp = lm(lifeexp ~ hlthpc)
library(jtools)
summ(ols.lifeexp, digits=3, confint = TRUE)
MODEL INFO:
Observations: 34
Dependent Variable: lifeexp
Type: OLS linear regression
MODEL FIT:
F(1,32) = 15.039, p = 0.000
R² = 0.320
Adj. R² = 0.298
Standard errors:OLS
-------------------------------------------------------------
Est. 2.5% 97.5% t val. p
----------------- -------- -------- -------- -------- -------
(Intercept) 73.084 70.997 75.170 71.355 0.000
hlthpc 0.001 0.001 0.002 3.878 0.000
-------------------------------------------------------------
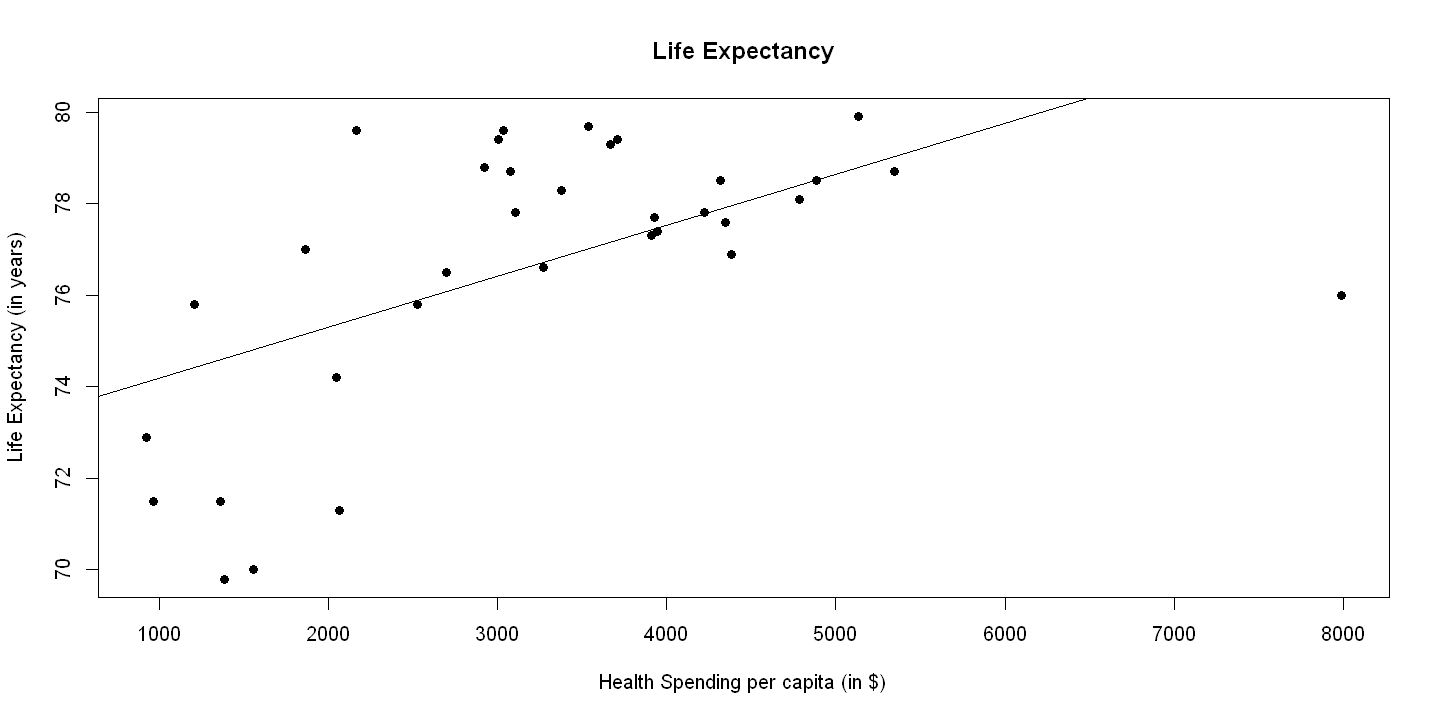
8.1.2. Figure 8.1 Panel A#
plot(hlthpc, lifeexp, xlab="Health Spending per capita (in $)",
ylab="Life Expectancy (in years)", pch=19, main="Life Expectancy")
abline(ols.lifeexp)
legend(1.5, 8, c("Actual", "Fitted"), lty=c(-1,1), pch=c(19,-1), bty="o")
Infant mortality. Key regression
ols.infmort = lm(infmort ~ hlthpc)
summ(ols.infmort, digits=3, confint = TRUE)
MODEL INFO:
Observations: 34
Dependent Variable: infmort
Type: OLS linear regression
MODEL FIT:
F(1,32) = 5.410, p = 0.027
R² = 0.145
Adj. R² = 0.118
Standard errors:OLS
-------------------------------------------------------------
Est. 2.5% 97.5% t val. p
----------------- -------- -------- -------- -------- -------
(Intercept) 6.702 4.535 8.869 6.300 0.000
hlthpc -0.001 -0.001 -0.000 -2.326 0.027
-------------------------------------------------------------
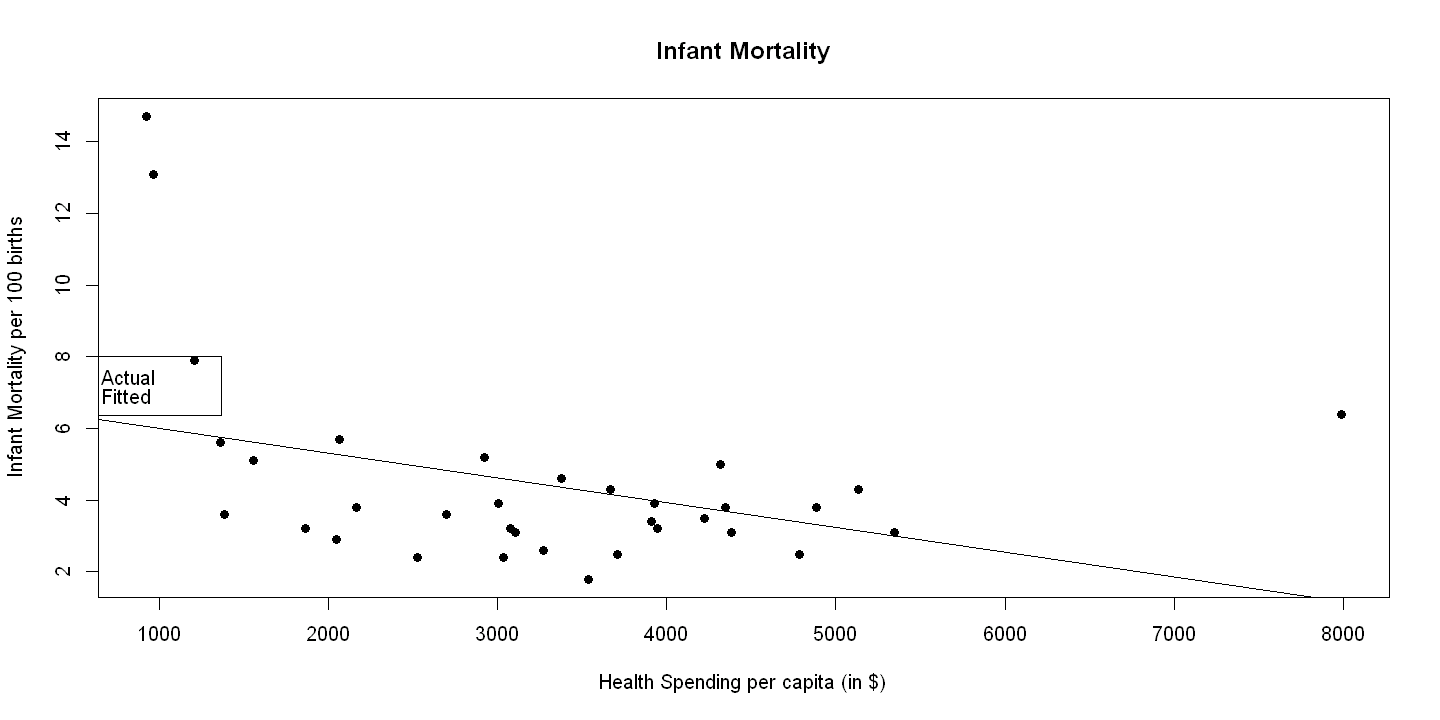
8.1.3. Figure 8.2 Panel B#
plot(hlthpc, infmort, xlab="Health Spending per capita (in $)",
ylab="Infant Mortality per 100 births", pch=19, main="Infant Mortality")
abline(ols.infmort)
legend(1.5, 8, c("Actual", "Fitted"), lty=c(-1,1), pch=c(19,-1), bty="o")
# Heteroscedastic-robust standard errors, uses package sandwich
summ(ols.lifeexp, digits=3, robust = "HC1")
summ(ols.infmort, digits=3, confint = TRUE, robust = "HC1")
MODEL INFO:
Observations: 34
Dependent Variable: lifeexp
Type: OLS linear regression
MODEL FIT:
F(1,32) = 15.039, p = 0.000
R² = 0.320
Adj. R² = 0.298
Standard errors: Robust, type = HC1
---------------------------------------------------
Est. S.E. t val. p
----------------- -------- ------- -------- -------
(Intercept) 73.084 1.565 46.697 0.000
hlthpc 0.001 0.000 2.398 0.023
---------------------------------------------------
MODEL INFO:
Observations: 34
Dependent Variable: infmort
Type: OLS linear regression
MODEL FIT:
F(1,32) = 5.410, p = 0.027
R² = 0.145
Adj. R² = 0.118
Standard errors: Robust, type = HC1
-------------------------------------------------------------
Est. 2.5% 97.5% t val. p
----------------- -------- -------- -------- -------- -------
(Intercept) 6.702 2.878 10.525 3.570 0.001
hlthpc -0.001 -0.002 0.000 -1.346 0.188
-------------------------------------------------------------
8.2. 8.2 HEALTH EXPENDITURES ACROSS COUNTRIES#
Same data as preceding
8.2.1. Table 8.2#
table82vars = c("gdppc", "hlthpc")
print(describe(df[table82vars]))
vars n mean sd median trimmed mad min max range skew kurtosis se
gdppc 1 34 33054.04 12916.75 32899.48 32057.63 8976.71 13806.16 82900.88 69094.72 1.50 4.32 2215.20
hlthpc 2 34 3255.65 1493.65 3188.50 3182.79 1600.47 923.00 7990.00 7067.00 0.67 0.96 256.16
Key regression
ols.hlthpc = lm(hlthpc ~ gdppc)
summ(ols.hlthpc, digits=3, confint = TRUE)
MODEL INFO:
Observations: 34
Dependent Variable: hlthpc
Type: OLS linear regression
MODEL FIT:
F(1,32) = 48.822, p = 0.000
R² = 0.604
Adj. R² = 0.592
Standard errors:OLS
------------------------------------------------------------------
Est. 2.5% 97.5% t val. p
----------------- --------- ---------- ---------- -------- -------
(Intercept) 284.906 -643.086 1212.898 0.625 0.536
gdppc 0.090 0.064 0.116 6.987 0.000
------------------------------------------------------------------
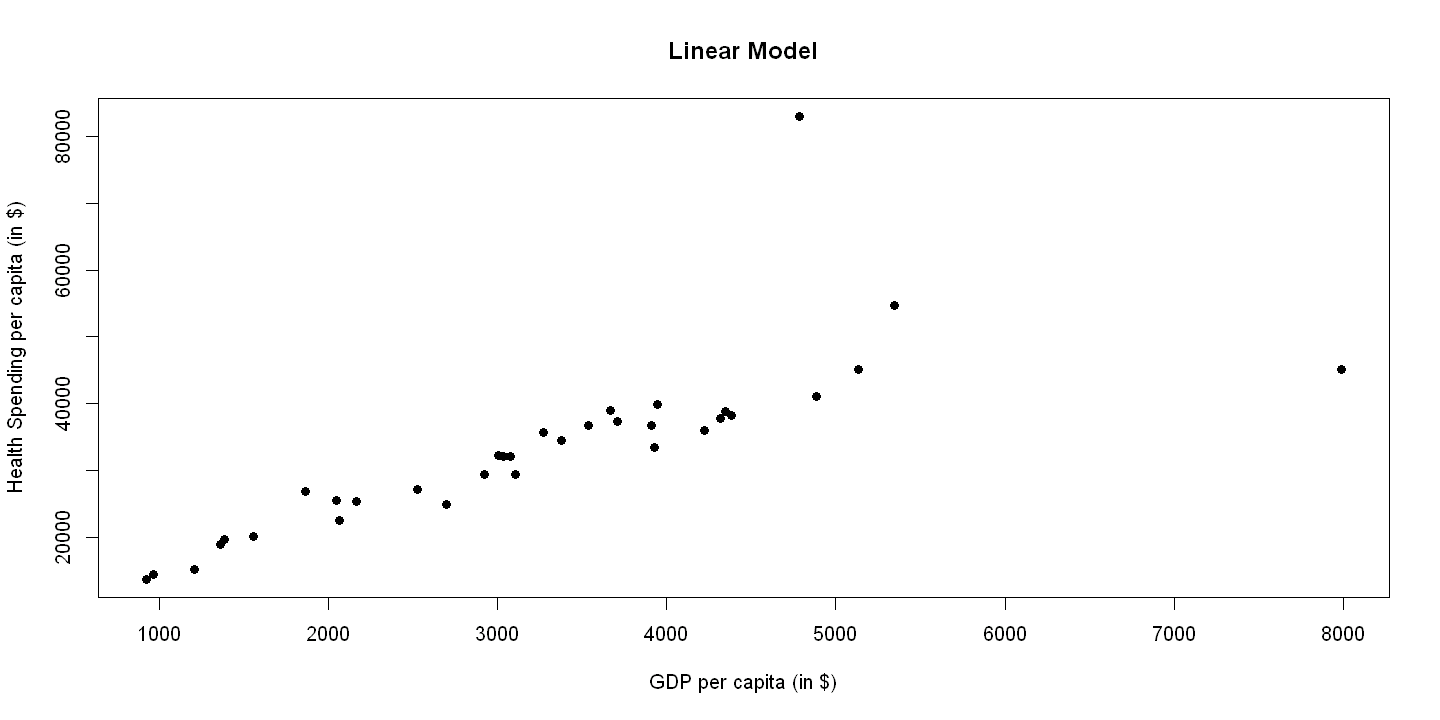
8.2.2. Figure 8.2 Panel A#
plot(hlthpc, gdppc, xlab="GDP per capita (in $)",
ylab="Health Spending per capita (in $)", pch=19, main="Linear Model")
abline(ols.hlthpc)
legend(1.5, 8, c("Actual", "Fitted"), lty=c(-1,1), pch=c(19,-1), bty="o")
Drop USA and Luxembourg for Figure 8,2. This works for summary statistic. But does not work for OLS
with(df[(df$code!="LUX") & (df$code!="USA"),],
summary(hlthpc) )
Min. 1st Qu. Median Mean 3rd Qu. Max.
923 2062 3091 3060 3934 5348
ols.hlthpc2 <- lm(hlthpc ~ gdppc, data=df[(df$code!="LUX") & (df$code!="USA"),])
summ(ols.hlthpc2)
MODEL INFO:
Observations: 32
Dependent Variable: hlthpc
Type: OLS linear regression
MODEL FIT:
F(1,30) = 387.79, p = 0.00
R² = 0.93
Adj. R² = 0.93
Standard errors:OLS
----------------------------------------------------
Est. S.E. t val. p
----------------- --------- -------- -------- ------
(Intercept) -883.31 208.95 -4.23 0.00
gdppc 0.13 0.01 19.69 0.00
----------------------------------------------------
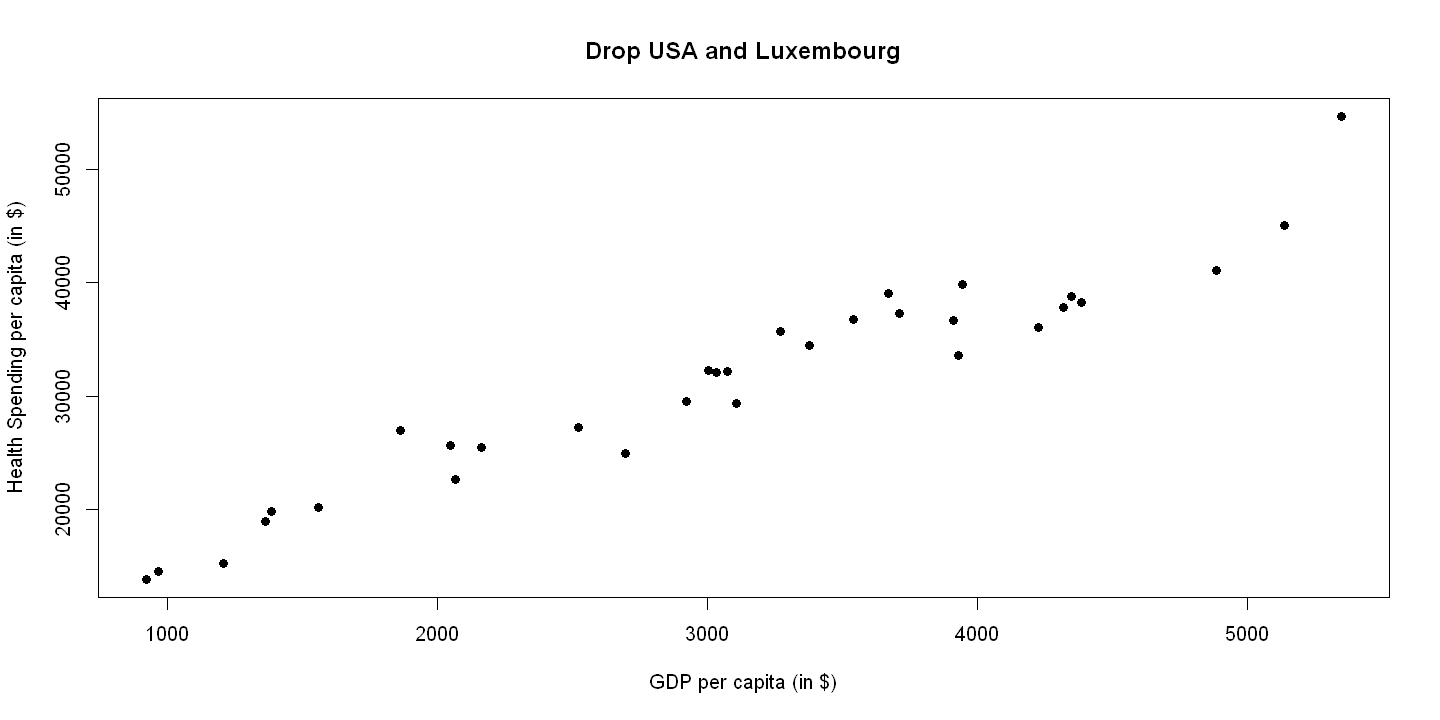
8.2.3. Figure 8.2 Panel B - I can get scatterplot but do not have line#
with(df[(df$code!="LUX") & (df$code!="USA"),],
plot(hlthpc, gdppc, xlab="GDP per capita (in $)",
ylab="Health Spending per capita (in $)", pch=19, main="Drop USA and Luxembourg") )
# Heteroskedastic-robust standard errors
summ(ols.hlthpc, digits=3, robust = "HC1")
summ(ols.hlthpc, digits=3, confint = TRUE, robust = "HC1")
MODEL INFO:
Observations: 34
Dependent Variable: hlthpc
Type: OLS linear regression
MODEL FIT:
F(1,32) = 48.822, p = 0.000
R² = 0.604
Adj. R² = 0.592
Standard errors: Robust, type = HC1
------------------------------------------------------
Est. S.E. t val. p
----------------- --------- --------- -------- -------
(Intercept) 284.906 862.354 0.330 0.743
gdppc 0.090 0.029 3.076 0.004
------------------------------------------------------
MODEL INFO:
Observations: 34
Dependent Variable: hlthpc
Type: OLS linear regression
MODEL FIT:
F(1,32) = 48.822, p = 0.000
R² = 0.604
Adj. R² = 0.592
Standard errors: Robust, type = HC1
-------------------------------------------------------------------
Est. 2.5% 97.5% t val. p
----------------- --------- ----------- ---------- -------- -------
(Intercept) 284.906 -1471.652 2041.464 0.330 0.743
gdppc 0.090 0.030 0.149 3.076 0.004
-------------------------------------------------------------------
8.3. 8.3 CAPM MODEL#
Date begins with month 280 in may 1983
rm(list=ls())
df = read.dta(file = "Dataset/AED_CAPM.DTA")
attach(df)
print(describe(df))
print(head(df))
vars n mean sd median trimmed mad min max range skew kurtosis se
date 1 354 456.50 102.34 456.50 456.50 131.21 280.00 633.00 353.00 0.00 -1.21 5.44
rm 2 354 0.01 0.05 0.01 0.01 0.04 -0.23 0.13 0.35 -0.86 2.61 0.00
rf 3 354 0.00 0.00 0.00 0.00 0.00 0.00 0.01 0.01 0.05 -0.71 0.00
rko 4 354 0.01 0.06 0.01 0.01 0.05 -0.19 0.22 0.41 -0.15 1.18 0.00
rtgt 5 354 0.01 0.08 0.01 0.01 0.07 -0.48 0.27 0.75 -0.40 3.04 0.00
rwmt 6 354 0.02 0.07 0.01 0.02 0.07 -0.27 0.26 0.53 -0.04 0.89 0.00
rm_rf 7 354 0.01 0.05 0.01 0.01 0.04 -0.23 0.12 0.36 -0.85 2.63 0.00
rko_rf 8 354 0.01 0.06 0.01 0.01 0.05 -0.20 0.22 0.41 -0.16 1.20 0.00
rtgt_rf 9 354 0.01 0.08 0.01 0.01 0.07 -0.48 0.26 0.75 -0.41 3.10 0.00
rwmt_rf 10 354 0.01 0.07 0.01 0.01 0.07 -0.28 0.26 0.54 -0.07 0.92 0.00
rm_rf_sq 11 354 0.00 0.00 0.00 0.00 0.00 0.00 0.05 0.05 6.93 67.64 0.00
smb 12 354 -0.13 3.16 -0.17 -0.07 2.45 -22.00 8.47 30.47 -1.33 8.28 0.17
hml 13 354 0.45 3.07 0.26 0.34 2.34 -9.78 13.84 23.62 0.54 2.37 0.16
date rm rf rko rtgt rwmt rm_rf rko_rf rtgt_rf rwmt_rf rm_rf_sq smb hml
1 280 0.0132 0.0069 -0.06780 0.022599 0.16438 0.0063 -0.07470 0.015699 0.15748 0.00003969 6.15 -1.40
2 281 0.0378 0.0067 -0.01818 0.077348 0.09412 0.0311 -0.02488 0.070648 0.08742 0.00096721 0.90 -3.87
3 282 -0.0316 0.0074 -0.07407 -0.020513 0.04301 -0.0390 -0.08147 -0.027913 0.03561 0.00152100 1.48 5.57
4 283 0.0035 0.0076 0.10000 -0.083770 -0.03093 -0.0041 0.09240 -0.091370 -0.03853 0.00001681 -4.28 5.55
5 284 0.0161 0.0076 0.00000 0.005714 0.03191 0.0085 -0.00760 -0.001886 0.02431 0.00007225 0.59 1.09
6 285 -0.0280 0.0076 0.03636 0.073864 -0.04124 -0.0356 0.02876 0.066264 -0.04884 0.00126736 -3.60 4.99
8.3.1. Table 8.3#
table83vars = c("rm", "rf", "rko", "rtgt", "rwmt", "rm_rf",
"rko_rf", "rtgt_rf", "rwmt_rf")
print(describe(df[table83vars]))
vars n mean sd median trimmed mad min max range skew kurtosis se
rm 1 354 0.01 0.05 0.01 0.01 0.04 -0.23 0.13 0.35 -0.86 2.61 0
rf 2 354 0.00 0.00 0.00 0.00 0.00 0.00 0.01 0.01 0.05 -0.71 0
rko 3 354 0.01 0.06 0.01 0.01 0.05 -0.19 0.22 0.41 -0.15 1.18 0
rtgt 4 354 0.01 0.08 0.01 0.01 0.07 -0.48 0.27 0.75 -0.40 3.04 0
rwmt 5 354 0.02 0.07 0.01 0.02 0.07 -0.27 0.26 0.53 -0.04 0.89 0
rm_rf 6 354 0.01 0.05 0.01 0.01 0.04 -0.23 0.12 0.36 -0.85 2.63 0
rko_rf 7 354 0.01 0.06 0.01 0.01 0.05 -0.20 0.22 0.41 -0.16 1.20 0
rtgt_rf 8 354 0.01 0.08 0.01 0.01 0.07 -0.48 0.26 0.75 -0.41 3.10 0
rwmt_rf 9 354 0.01 0.07 0.01 0.01 0.07 -0.28 0.26 0.54 -0.07 0.92 0
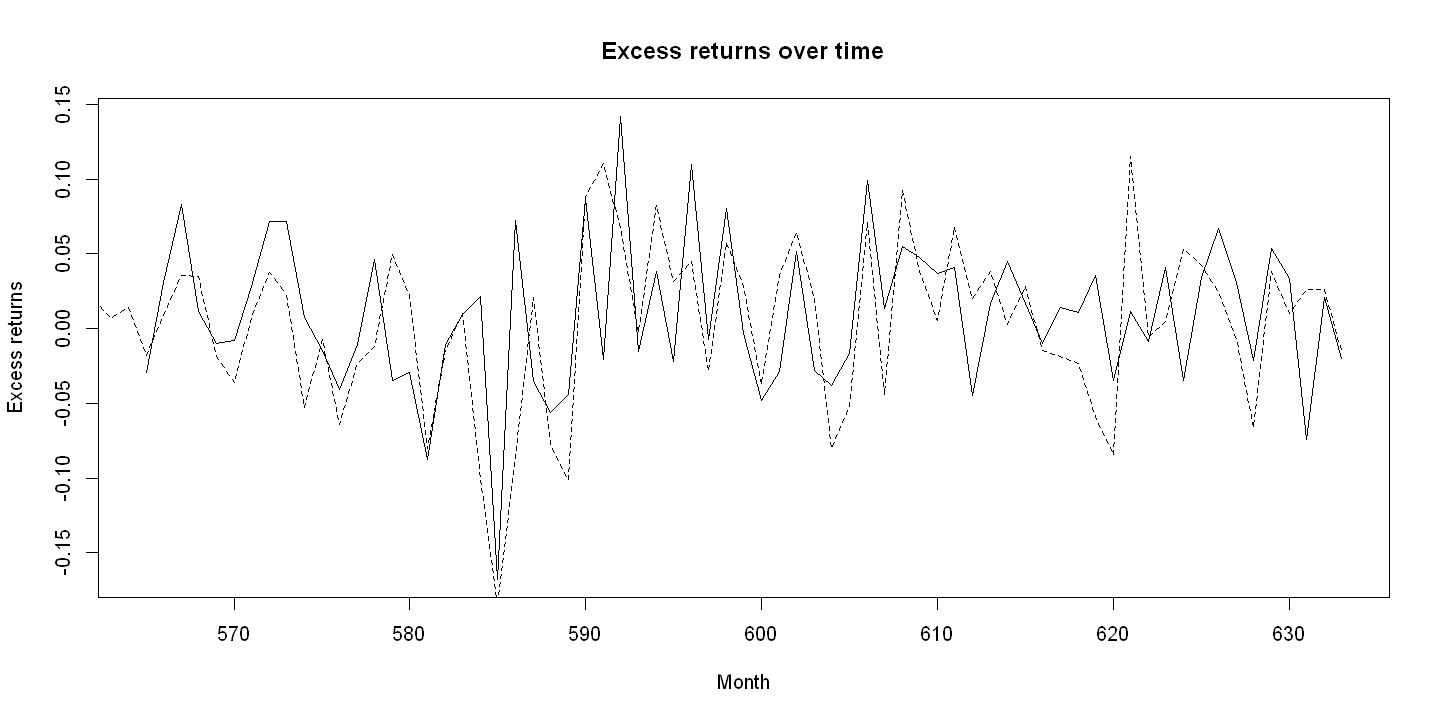
8.3.2. Figure 8.3 panel A#
For readability use only the last 20% of data in the first panel. This begins with observation 285 which is monthly date = 565
with(df[date>=565,],
plot(date, rko_rf, xlab="Month", ylab="Excess returns",
main="Excess returns over time", type="l", lty=1))
points(date, rm_rf, type="l", lty=2)
Key regression
ols.capm = lm(rko_rf ~ rm_rf)
summ(ols.capm, digits=4)
MODEL INFO:
Observations: 354
Dependent Variable: rko_rf
Type: OLS linear regression
MODEL FIT:
F(1,352) = 88.5805, p = 0.0000
R² = 0.2011
Adj. R² = 0.1988
Standard errors:OLS
-----------------------------------------------------
Est. S.E. t val. p
----------------- -------- -------- -------- --------
(Intercept) 0.0068 0.0030 2.3071 0.0216
rm_rf 0.6063 0.0644 9.4117 0.0000
-----------------------------------------------------
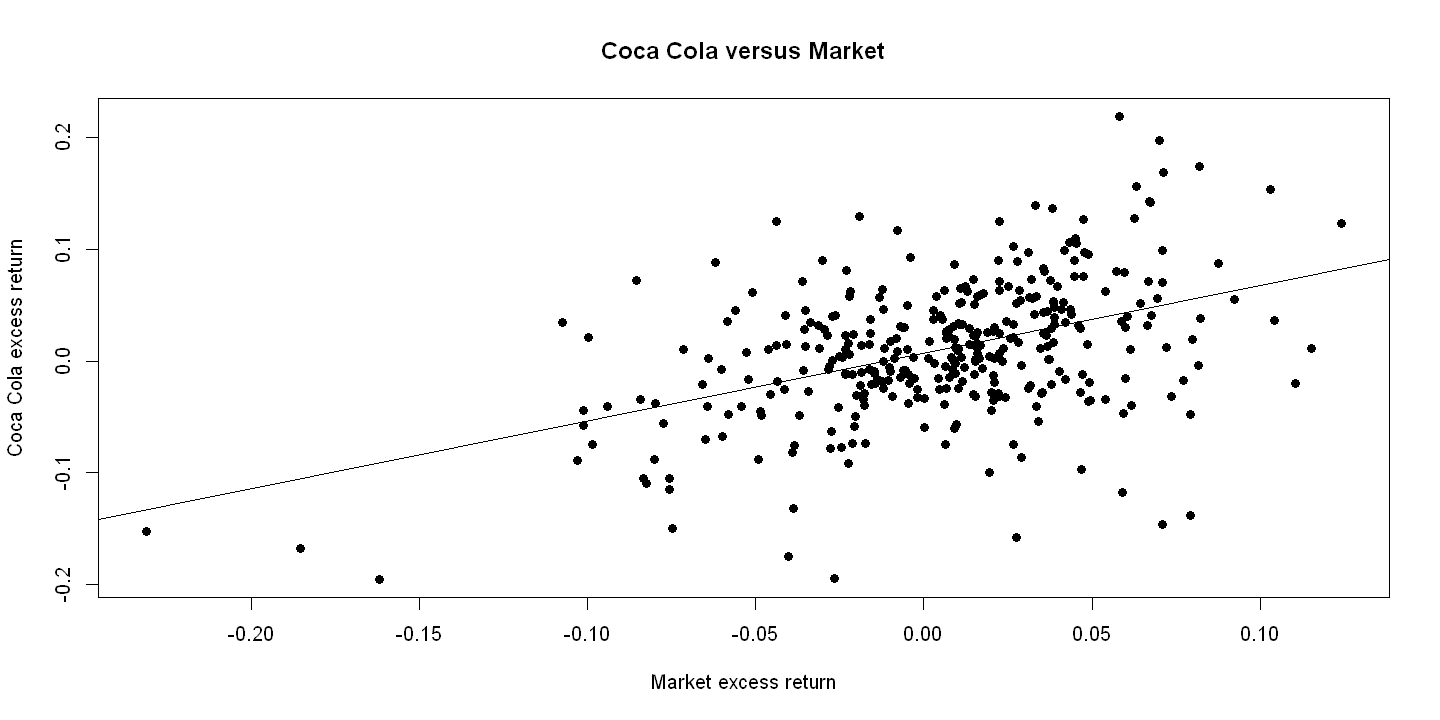
8.3.3. Figure 8.3 Panel B#
plot(rm_rf, rko_rf, xlab="Market excess return",
ylab="Coca Cola excess return", pch=19, main="Coca Cola versus Market")
abline(ols.capm)
legend(1.5, 8, c("Actual", "Fitted"), lty=c(-1,1), pch=c(19,-1), bty="o")
# Heteroscedastic-robust standard errors
summ(ols.capm, digits=3, robust = "HC1")
MODEL INFO:
Observations: 354
Dependent Variable: rko_rf
Type: OLS linear regression
MODEL FIT:
F(1,352) = 88.581, p = 0.000
R² = 0.201
Adj. R² = 0.199
Standard errors: Robust, type = HC1
--------------------------------------------------
Est. S.E. t val. p
----------------- ------- ------- -------- -------
(Intercept) 0.007 0.003 2.351 0.019
rm_rf 0.606 0.077 7.877 0.000
--------------------------------------------------
8.4. 8.4 OUTPUT AND UMEMPLOYMENT IN THE U.S.#
rm(list=ls())
df = read.dta(file = "Dataset/AED_GDPUNEMPLOY.DTA")
attach(df)
print(describe(df))
print(head(df))
The following object is masked from df (pos = 5):
year
vars n mean sd median trimmed mad min max range skew kurtosis se
year 1 59 1990.00 17.18 1990.00 1990.00 22.24 1961.00 2019.00 58.00 0.00 -1.26 2.24
urate 2 59 6.05 1.63 5.69 5.93 1.60 3.56 9.86 6.30 0.64 -0.28 0.21
rgdp 3 59 10114.22 4735.26 9355.35 9941.73 5889.00 3343.55 19073.06 15729.51 0.29 -1.32 616.48
rgdpgrowth 4 59 3.06 2.04 3.12 3.14 1.84 -2.54 7.24 9.77 -0.45 0.12 0.27
uratechange 5 59 -0.03 0.99 -0.30 -0.14 0.61 -2.14 3.53 5.67 1.34 2.41 0.13
year urate rgdp rgdpgrowth uratechange
1 1961 6.770271 3343.546 2.563673 1.1531562
2 1962 5.596210 3548.409 6.127118 -1.1740603
3 1963 5.739126 3702.944 4.355051 0.1429152
4 1964 5.246175 3916.280 5.761254 -0.4929504
5 1965 4.579955 4170.750 6.497748 -0.6662202
6 1966 3.832191 4445.853 6.596008 -0.7477641
8.4.1. Table 8.4#
table84vars = c("rgdpgrowth", "uratechange")
print(describe(df[table84vars]))
vars n mean sd median trimmed mad min max range skew kurtosis se
rgdpgrowth 1 59 3.06 2.04 3.12 3.14 1.84 -2.54 7.24 9.77 -0.45 0.12 0.27
uratechange 2 59 -0.03 0.99 -0.30 -0.14 0.61 -2.14 3.53 5.67 1.34 2.41 0.13
Key regression
ols.okun = lm(rgdpgrowth ~ uratechange)
summ(ols.okun, digits=3)
MODEL INFO:
Observations: 59
Dependent Variable: rgdpgrowth
Type: OLS linear regression
MODEL FIT:
F(1,57) = 82.718, p = 0.000
R² = 0.592
Adj. R² = 0.585
Standard errors:OLS
---------------------------------------------------
Est. S.E. t val. p
----------------- -------- ------- -------- -------
(Intercept) 3.008 0.171 17.589 0.000
uratechange -1.589 0.175 -9.095 0.000
---------------------------------------------------
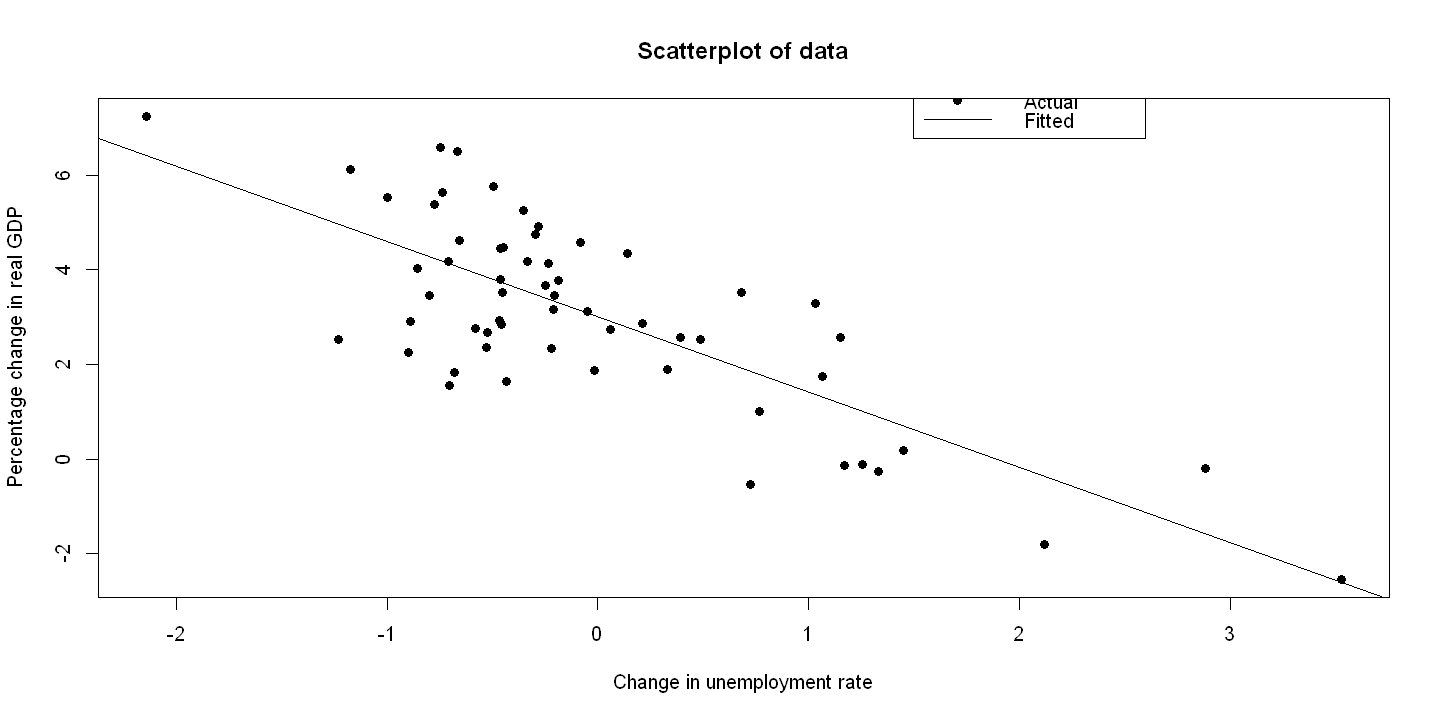
8.4.2. Figure 8.4 Panel A#
plot(uratechange, rgdpgrowth, xlab="Change in unemployment rate",
ylab="Percentage change in real GDP", pch=19, main="Scatterplot of data")
abline(ols.okun)
legend(1.5, 8, c("Actual", "Fitted"), lty=c(-1,1), pch=c(19,-1), bty="o")
Get predictions
pgrowth = predict(ols.okun)
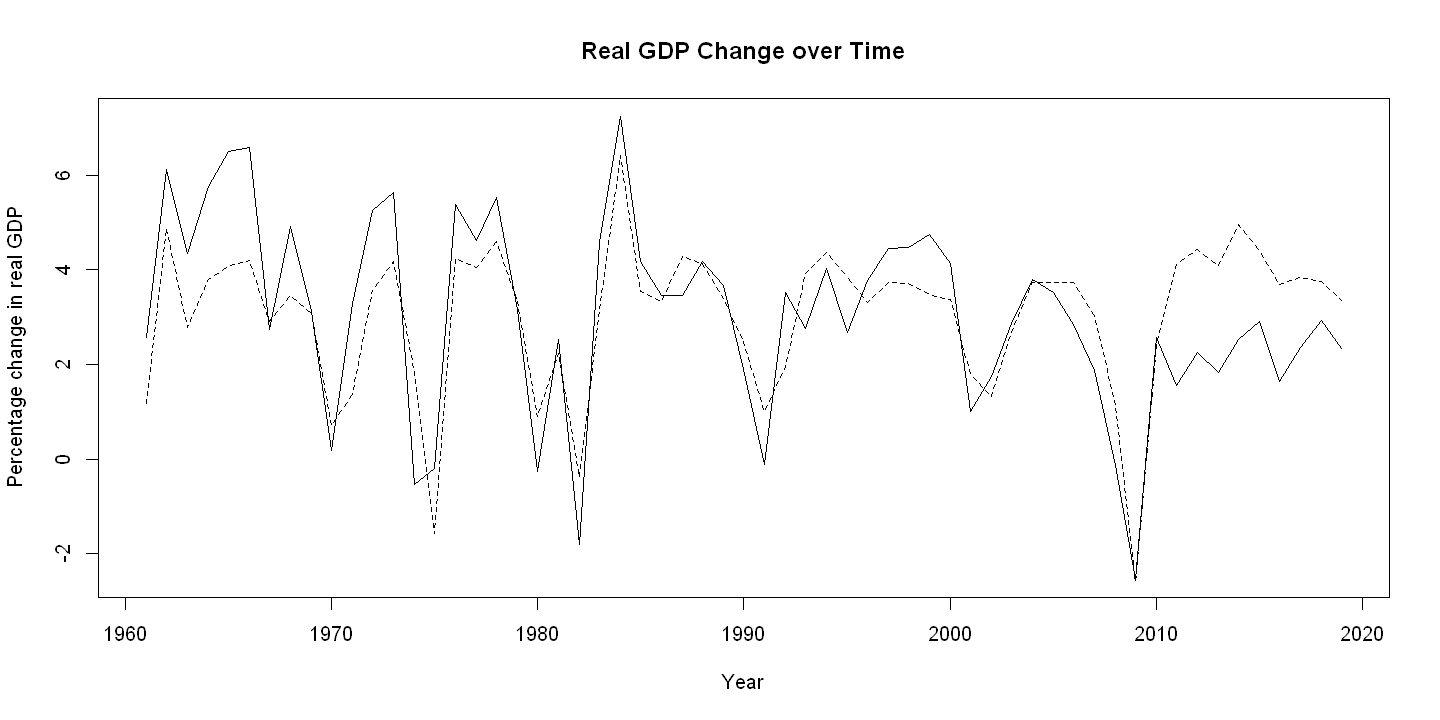
8.4.3. Figure 8.4 Panel B#
plot(year, rgdpgrowth, xlab="Year", ylab="Percentage change in real GDP",
main="Real GDP Change over Time", type="l", lty=1)
points(year, pgrowth, type="l", lty=2)
# Heteroscedastic-robust standard errors
summ(ols.okun, digits=3, robust = "HC1")
MODEL INFO:
Observations: 59
Dependent Variable: rgdpgrowth
Type: OLS linear regression
MODEL FIT:
F(1,57) = 82.718, p = 0.000
R² = 0.592
Adj. R² = 0.585
Standard errors: Robust, type = HC1
---------------------------------------------------
Est. S.E. t val. p
----------------- -------- ------- -------- -------
(Intercept) 3.008 0.170 17.688 0.000
uratechange -1.589 0.163 -9.749 0.000
---------------------------------------------------