9 CHAPTER 9: MODELLING VOLATILITY AND CORRELATION
9.1 Estimating the GARCH(1,1) model (Page 438)
library("foreign")
data = read.dta("Dataset/currencies.dta")
data = na.omit(data)
library("rugarch")
garch11.spec = ugarchspec(mean.model=list(armaOrder=c(0,0)),
variance.model=list(garchOrder=c(1,1),model="sGARCH"))
garch11.fit = ugarchfit(garch11.spec,data=data$rjpy)
garch11.fit
##
## *---------------------------------*
## * GARCH Model Fit *
## *---------------------------------*
##
## Conditional Variance Dynamics
## -----------------------------------
## GARCH Model : sGARCH(1,1)
## Mean Model : ARFIMA(0,0,0)
## Distribution : norm
##
## Optimal Parameters
## ------------------------------------
## Estimate Std. Error t value Pr(>|t|)
## mu 0.002546 0.006769 0.37612 0.706828
## omega 0.004489 0.001126 3.98853 0.000066
## alpha1 0.047579 0.008082 5.88696 0.000000
## beta1 0.932508 0.011884 78.46766 0.000000
##
## Robust Standard Errors:
## Estimate Std. Error t value Pr(>|t|)
## mu 0.002546 0.008090 0.31472 0.752974
## omega 0.004489 0.002849 1.57558 0.115123
## alpha1 0.047579 0.019477 2.44282 0.014573
## beta1 0.932508 0.028282 32.97212 0.000000
##
## LogLikelihood : -2460.987
##
## Information Criteria
## ------------------------------------
##
## Akaike 1.2365
## Bayes 1.2428
## Shibata 1.2365
## Hannan-Quinn 1.2387
##
## Weighted Ljung-Box Test on Standardized Residuals
## ------------------------------------
## statistic p-value
## Lag[1] 102.5 0
## Lag[2*(p+q)+(p+q)-1][2] 103.6 0
## Lag[4*(p+q)+(p+q)-1][5] 106.8 0
## d.o.f=0
## H0 : No serial correlation
##
## Weighted Ljung-Box Test on Standardized Squared Residuals
## ------------------------------------
## statistic p-value
## Lag[1] 13.72 2.119e-04
## Lag[2*(p+q)+(p+q)-1][5] 17.81 7.692e-05
## Lag[4*(p+q)+(p+q)-1][9] 21.34 9.024e-05
## d.o.f=2
##
## Weighted ARCH LM Tests
## ------------------------------------
## Statistic Shape Scale P-Value
## ARCH Lag[3] 3.514 0.500 2.000 0.06087
## ARCH Lag[5] 7.623 1.440 1.667 0.02472
## ARCH Lag[7] 9.455 2.315 1.543 0.02460
##
## Nyblom stability test
## ------------------------------------
## Joint Statistic: 0.7864
## Individual Statistics:
## mu 0.18508
## omega 0.08219
## alpha1 0.09814
## beta1 0.11643
##
## Asymptotic Critical Values (10% 5% 1%)
## Joint Statistic: 1.07 1.24 1.6
## Individual Statistic: 0.35 0.47 0.75
##
## Sign Bias Test
## ------------------------------------
## t-value prob sig
## Sign Bias 0.08355 9.334e-01
## Negative Sign Bias 4.82315 1.466e-06 ***
## Positive Sign Bias 1.65357 9.829e-02 *
## Joint Effect 29.68720 1.606e-06 ***
##
##
## Adjusted Pearson Goodness-of-Fit Test:
## ------------------------------------
## group statistic p-value(g-1)
## 1 20 847.9 1.378e-167
## 2 30 1084.9 9.530e-210
## 3 40 1291.6 1.213e-245
## 4 50 1426.0 2.061e-266
##
##
## Elapsed time : 0.2749989
9.2 GJR (‘threshold’ GARCH) (Page 442)
gjrgarch11.spec = ugarchspec(mean.model=list(armaOrder=c(0,0)),
variance.model=list(garchOrder=c(1,1),model="gjrGARCH"))
gjrgarch11.fit = ugarchfit(gjrgarch11.spec,data=data$rjpy)
gjrgarch11.fit
##
## *---------------------------------*
## * GARCH Model Fit *
## *---------------------------------*
##
## Conditional Variance Dynamics
## -----------------------------------
## GARCH Model : gjrGARCH(1,1)
## Mean Model : ARFIMA(0,0,0)
## Distribution : norm
##
## Optimal Parameters
## ------------------------------------
## Estimate Std. Error t value Pr(>|t|)
## mu -0.001369 0.006765 -0.20233 0.839658
## omega 0.003956 0.000938 4.21785 0.000025
## alpha1 0.025541 0.006127 4.16871 0.000031
## beta1 0.937628 0.010070 93.11060 0.000000
## gamma1 0.038786 0.008537 4.54342 0.000006
##
## Robust Standard Errors:
## Estimate Std. Error t value Pr(>|t|)
## mu -0.001369 0.008004 -0.17102 0.864209
## omega 0.003956 0.002096 1.88760 0.059080
## alpha1 0.025541 0.011676 2.18744 0.028710
## beta1 0.937628 0.020423 45.90967 0.000000
## gamma1 0.038786 0.017662 2.19596 0.028095
##
## LogLikelihood : -2447.737
##
## Information Criteria
## ------------------------------------
##
## Akaike 1.2304
## Bayes 1.2383
## Shibata 1.2304
## Hannan-Quinn 1.2332
##
## Weighted Ljung-Box Test on Standardized Residuals
## ------------------------------------
## statistic p-value
## Lag[1] 108.4 0
## Lag[2*(p+q)+(p+q)-1][2] 109.3 0
## Lag[4*(p+q)+(p+q)-1][5] 112.7 0
## d.o.f=0
## H0 : No serial correlation
##
## Weighted Ljung-Box Test on Standardized Squared Residuals
## ------------------------------------
## statistic p-value
## Lag[1] 10.95 0.0009360
## Lag[2*(p+q)+(p+q)-1][5] 15.34 0.0003597
## Lag[4*(p+q)+(p+q)-1][9] 19.76 0.0002321
## d.o.f=2
##
## Weighted ARCH LM Tests
## ------------------------------------
## Statistic Shape Scale P-Value
## ARCH Lag[3] 3.393 0.500 2.000 0.06547
## ARCH Lag[5] 8.179 1.440 1.667 0.01818
## ARCH Lag[7] 10.879 2.315 1.543 0.01146
##
## Nyblom stability test
## ------------------------------------
## Joint Statistic: 1.4159
## Individual Statistics:
## mu 0.14156
## omega 0.09306
## alpha1 0.10686
## beta1 0.11944
## gamma1 0.08167
##
## Asymptotic Critical Values (10% 5% 1%)
## Joint Statistic: 1.28 1.47 1.88
## Individual Statistic: 0.35 0.47 0.75
##
## Sign Bias Test
## ------------------------------------
## t-value prob sig
## Sign Bias 1.393 1.638e-01
## Negative Sign Bias 3.204 1.364e-03 ***
## Positive Sign Bias 2.727 6.429e-03 ***
## Joint Effect 23.302 3.494e-05 ***
##
##
## Adjusted Pearson Goodness-of-Fit Test:
## ------------------------------------
## group statistic p-value(g-1)
## 1 20 818.6 2.444e-161
## 2 30 998.8 1.574e-191
## 3 40 1138.9 1.757e-213
## 4 50 1275.1 8.706e-235
##
##
## Elapsed time : 0.4268448
9.3 EGARCH (Page 443)
egarch11.spec = ugarchspec(mean.model=list(armaOrder=c(0,0)),
variance.model=list(garchOrder=c(1,1),model="eGARCH"))
egarch11.fit = ugarchfit(egarch11.spec,data=data$rjpy)
egarch11.fit
##
## *---------------------------------*
## * GARCH Model Fit *
## *---------------------------------*
##
## Conditional Variance Dynamics
## -----------------------------------
## GARCH Model : eGARCH(1,1)
## Mean Model : ARFIMA(0,0,0)
## Distribution : norm
##
## Optimal Parameters
## ------------------------------------
## Estimate Std. Error t value Pr(>|t|)
## mu -0.001276 0.002104 -0.60618 0.544393
## omega -0.022104 0.013013 -1.69861 0.089393
## alpha1 -0.037615 0.011148 -3.37416 0.000740
## beta1 0.979362 0.009578 102.24797 0.000000
## gamma1 0.108134 0.025814 4.18895 0.000028
##
## Robust Standard Errors:
## Estimate Std. Error t value Pr(>|t|)
## mu -0.001276 0.000962 -1.32584 0.18489
## omega -0.022104 0.059750 -0.36994 0.71142
## alpha1 -0.037615 0.050061 -0.75138 0.45243
## beta1 0.979362 0.044902 21.81124 0.00000
## gamma1 0.108134 0.114671 0.94300 0.34568
##
## LogLikelihood : -2443.073
##
## Information Criteria
## ------------------------------------
##
## Akaike 1.2280
## Bayes 1.2359
## Shibata 1.2280
## Hannan-Quinn 1.2308
##
## Weighted Ljung-Box Test on Standardized Residuals
## ------------------------------------
## statistic p-value
## Lag[1] 111.3 0
## Lag[2*(p+q)+(p+q)-1][2] 112.3 0
## Lag[4*(p+q)+(p+q)-1][5] 115.8 0
## d.o.f=0
## H0 : No serial correlation
##
## Weighted Ljung-Box Test on Standardized Squared Residuals
## ------------------------------------
## statistic p-value
## Lag[1] 12.44 0.0004207
## Lag[2*(p+q)+(p+q)-1][5] 16.28 0.0002013
## Lag[4*(p+q)+(p+q)-1][9] 20.74 0.0001291
## d.o.f=2
##
## Weighted ARCH LM Tests
## ------------------------------------
## Statistic Shape Scale P-Value
## ARCH Lag[3] 2.957 0.500 2.000 0.08552
## ARCH Lag[5] 7.236 1.440 1.667 0.03060
## ARCH Lag[7] 10.357 2.315 1.543 0.01520
##
## Nyblom stability test
## ------------------------------------
## Joint Statistic: 1.1567
## Individual Statistics:
## mu 0.05683
## omega 0.09884
## alpha1 0.23824
## beta1 0.08921
## gamma1 0.13344
##
## Asymptotic Critical Values (10% 5% 1%)
## Joint Statistic: 1.28 1.47 1.88
## Individual Statistic: 0.35 0.47 0.75
##
## Sign Bias Test
## ------------------------------------
## t-value prob sig
## Sign Bias 1.101 2.712e-01
## Negative Sign Bias 3.425 6.221e-04 ***
## Positive Sign Bias 2.649 8.104e-03 ***
## Joint Effect 23.431 3.283e-05 ***
##
##
## Adjusted Pearson Goodness-of-Fit Test:
## ------------------------------------
## group statistic p-value(g-1)
## 1 20 820.0 1.211e-161
## 2 30 989.4 1.483e-189
## 3 40 1132.0 4.906e-212
## 4 50 1289.9 6.899e-238
##
##
## Elapsed time : 0.3589249
garch11.ni = newsimpact(garch11.fit)
gjrgarch11.ni = newsimpact(gjrgarch11.fit)
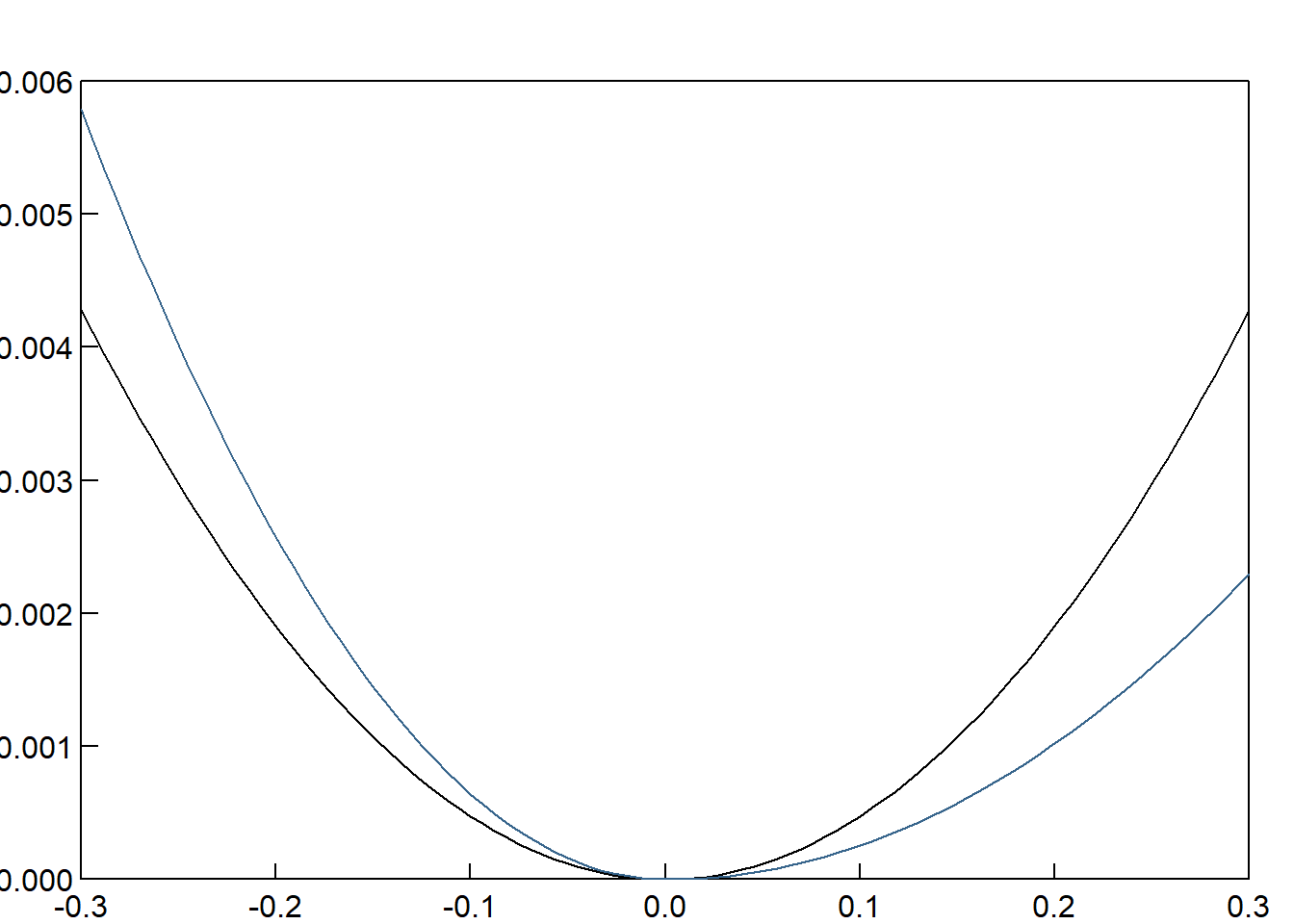
9.4 FIGURE 9.3. (Page 445)
News impact curves for S&P500 returns coefficients implied from GARCH and GJR model estimates
par(mfcol = c(1,1), oma = c(0,0,1,0) + 0.2, mar = c(0,1,0,0) + 1, mgp = c(0, 0.2, 0))
plot(garch11.ni$zx,garch11.ni$zy-min(abs(garch11.ni$zy)),type="l",las=1,xlab="",ylab="",main="",xaxs="i",yaxs="i",tck=.02,ylim=c(0,0.006))
lines(gjrgarch11.ni$zx,gjrgarch11.ni$zy-min(abs(gjrgarch11.ni$zy)),col="steelblue4")
9.5 GARCH-in-mean (Page 446)
garchm11.spec = ugarchspec(mean.model=list(armaOrder=c(0,0),archm=TRUE,archpow=1),
variance.model=list(garchOrder=c(1,1),model="sGARCH"))
garchm11.fit = ugarchfit(garchm11.spec,data=data$rjpy)
garchm11.fit
##
## *---------------------------------*
## * GARCH Model Fit *
## *---------------------------------*
##
## Conditional Variance Dynamics
## -----------------------------------
## GARCH Model : sGARCH(1,1)
## Mean Model : ARFIMA(0,0,0)
## Distribution : norm
##
## Optimal Parameters
## ------------------------------------
## Estimate Std. Error t value Pr(>|t|)
## mu 0.024452 0.034364 0.71155 0.476743
## archm -0.051739 0.079680 -0.64934 0.516121
## omega 0.004409 0.001117 3.94612 0.000079
## alpha1 0.047424 0.008052 5.88950 0.000000
## beta1 0.933047 0.011815 78.97247 0.000000
##
## Robust Standard Errors:
## Estimate Std. Error t value Pr(>|t|)
## mu 0.024452 0.042288 0.57822 0.563115
## archm -0.051739 0.095217 -0.54338 0.586870
## omega 0.004409 0.002816 1.56598 0.117352
## alpha1 0.047424 0.019557 2.42491 0.015312
## beta1 0.933047 0.028292 32.97891 0.000000
##
## LogLikelihood : -2460.776
##
## Information Criteria
## ------------------------------------
##
## Akaike 1.2369
## Bayes 1.2448
## Shibata 1.2369
## Hannan-Quinn 1.2397
##
## Weighted Ljung-Box Test on Standardized Residuals
## ------------------------------------
## statistic p-value
## Lag[1] 102.7 0
## Lag[2*(p+q)+(p+q)-1][2] 103.8 0
## Lag[4*(p+q)+(p+q)-1][5] 107.0 0
## d.o.f=0
## H0 : No serial correlation
##
## Weighted Ljung-Box Test on Standardized Squared Residuals
## ------------------------------------
## statistic p-value
## Lag[1] 14.02 1.812e-04
## Lag[2*(p+q)+(p+q)-1][5] 18.07 6.541e-05
## Lag[4*(p+q)+(p+q)-1][9] 21.60 7.757e-05
## d.o.f=2
##
## Weighted ARCH LM Tests
## ------------------------------------
## Statistic Shape Scale P-Value
## ARCH Lag[3] 3.478 0.500 2.000 0.06218
## ARCH Lag[5] 7.552 1.440 1.667 0.02571
## ARCH Lag[7] 9.400 2.315 1.543 0.02532
##
## Nyblom stability test
## ------------------------------------
## Joint Statistic: 0.7806
## Individual Statistics:
## mu 0.15261
## archm 0.15783
## omega 0.08669
## alpha1 0.09929
## beta1 0.12005
##
## Asymptotic Critical Values (10% 5% 1%)
## Joint Statistic: 1.28 1.47 1.88
## Individual Statistic: 0.35 0.47 0.75
##
## Sign Bias Test
## ------------------------------------
## t-value prob sig
## Sign Bias 0.4557 6.486e-01
## Negative Sign Bias 4.6212 3.937e-06 ***
## Positive Sign Bias 1.8567 6.343e-02 *
## Joint Effect 30.2116 1.246e-06 ***
##
##
## Adjusted Pearson Goodness-of-Fit Test:
## ------------------------------------
## group statistic p-value(g-1)
## 1 20 778.1 9.575e-153
## 2 30 969.4 2.481e-185
## 3 40 1156.7 3.103e-217
## 4 50 1252.4 4.850e-230
##
##
## Elapsed time : 0.678983
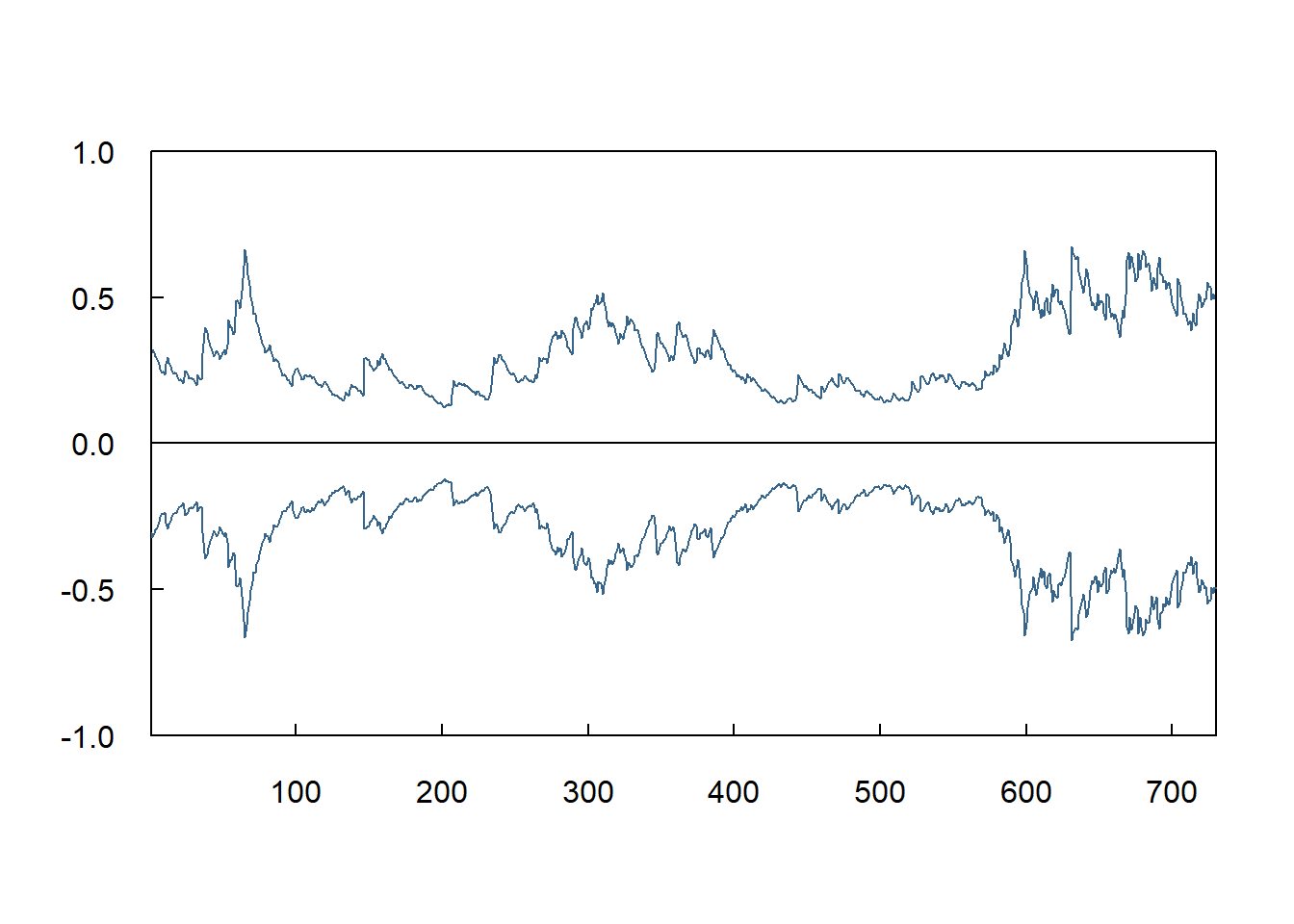
9.6 Screenshot 9.4 Dynamic forecasts of the conditional variance (Page 450)
egarch11.fore = ugarchforecast(egarch11.fit,n.ahead=730)
lower =-1.65*egarch11.fore@forecast$sigmaFor
upper = 1.65*egarch11.fore@forecast$sigmaFor
plot(lower,type="l",las=1,xlab="",ylab="",main="",xaxs="i",yaxs="i",tck=.02,ylim=c(-1,1),col="steelblue4")
lines(upper,col="steelblue4")
abline(h=0)
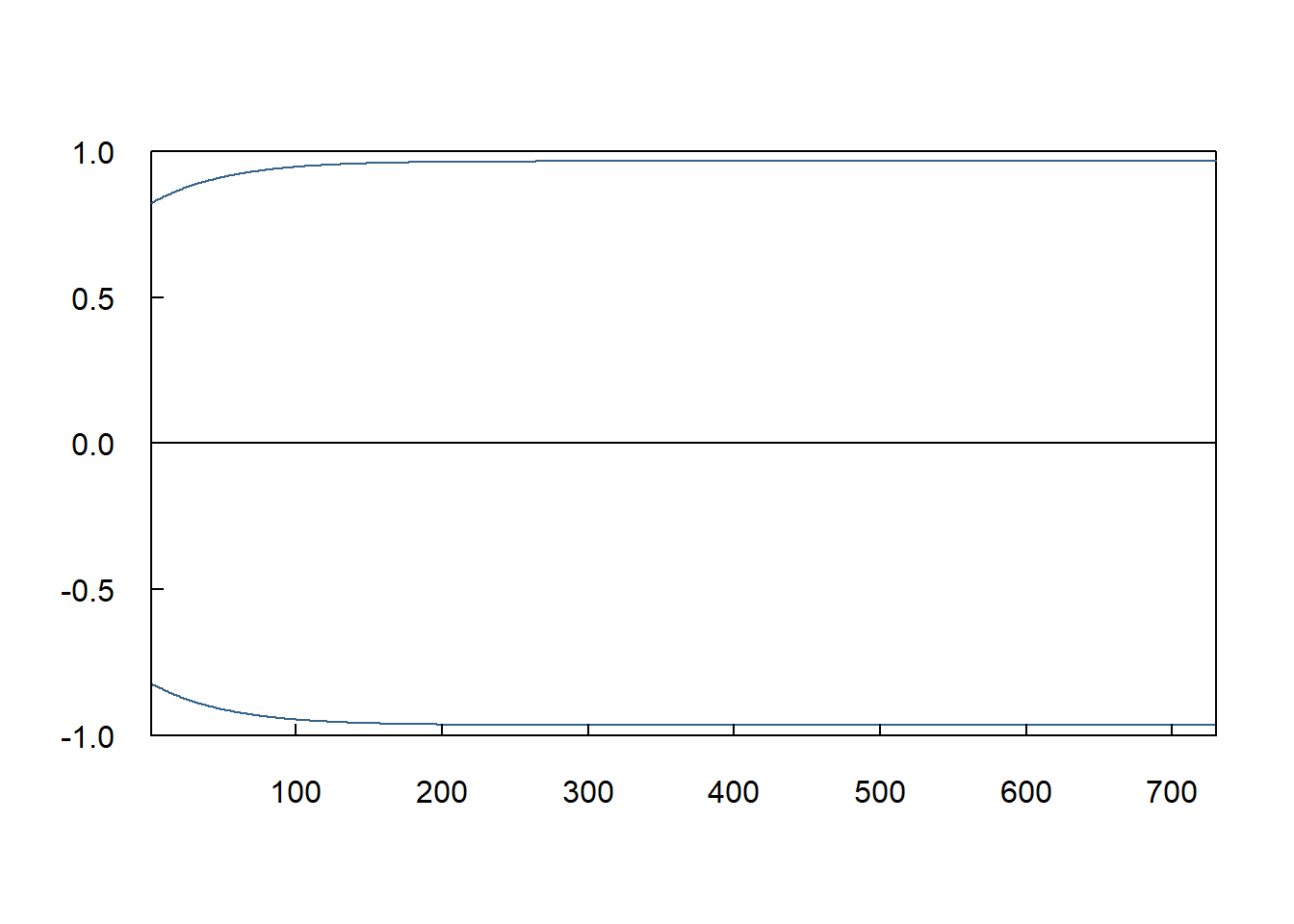
9.7 Screenshot 9.5 Static forecasts of the conditional variance (Page 451)
library(xts)
# Ensure 'data' has a Date column
rjpy_xts <- xts(data$rjpy, order.by = data$Date)
space <- 730
sigma.fore <- numeric(space)
for (i in 1:space) {
dynamic.egarch.fit <- ugarchfit(egarch11.spec, rjpy_xts[1:(nrow(rjpy_xts)-space+i)])
sigma.fore[i] <- ugarchforecast(dynamic.egarch.fit, n.ahead = 1)@forecast$sigmaFor
if (i %% 50 == 0) {
print(i / space * 100)
}
}
## [1] 6.849315
## [1] 13.69863
## [1] 20.54795
## [1] 27.39726
## [1] 34.24658
## [1] 41.09589
## [1] 47.94521
## [1] 54.79452
## [1] 61.64384
## [1] 68.49315
## [1] 75.34247
## [1] 82.19178
## [1] 89.0411
## [1] 95.89041
plot(2 * sigma.fore^2, type = "l", las = 1, xlab = "", ylab = "",
main = "", xaxs = "i", yaxs = "i", tck = .02, col = "steelblue4", ylim = c(-1, 1))
lines(-2 * sigma.fore^2, col = "steelblue4")
abline(h = 0)