Testing for unit roots (Page 371)
library("foreign")
data = read.dta("Dataset/ukhp.dta")
library("urca")
df.hp = ur.df(data$HP,type="drift",lags=2)
df.hp@testreg
##
## Call:
## lm(formula = z.diff ~ z.lag.1 + 1 + z.diff.lag)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4825.5 -618.4 -22.6 629.0 4787.3
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 2.345e+02 1.768e+02 1.326 0.186
## z.lag.1 -6.858e-04 1.458e-03 -0.470 0.639
## z.diff.lag1 3.162e-01 5.837e-02 5.417 1.37e-07 ***
## z.diff.lag2 3.332e-01 5.840e-02 5.706 3.12e-08 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1187 on 262 degrees of freedom
## Multiple R-squared: 0.3086, Adjusted R-squared: 0.3007
## F-statistic: 38.98 on 3 and 262 DF, p-value: < 2.2e-16
Testing for unit roots (Page 372)
df.dhp = ur.df(diff(data$HP),type="drift",lags=1)
df.dhp@testreg
##
## Call:
## lm(formula = z.diff ~ z.lag.1 + 1 + z.diff.lag)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4873.3 -595.6 -15.6 632.7 4759.0
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 159.66720 76.90883 2.076 0.0389 *
## z.lag.1 -0.35126 0.05996 -5.858 1.40e-08 ***
## z.diff.lag -0.33262 0.05830 -5.706 3.12e-08 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1185 on 263 degrees of freedom
## Multiple R-squared: 0.3437, Adjusted R-squared: 0.3387
## F-statistic: 68.87 on 2 and 263 DF, p-value: < 2.2e-16
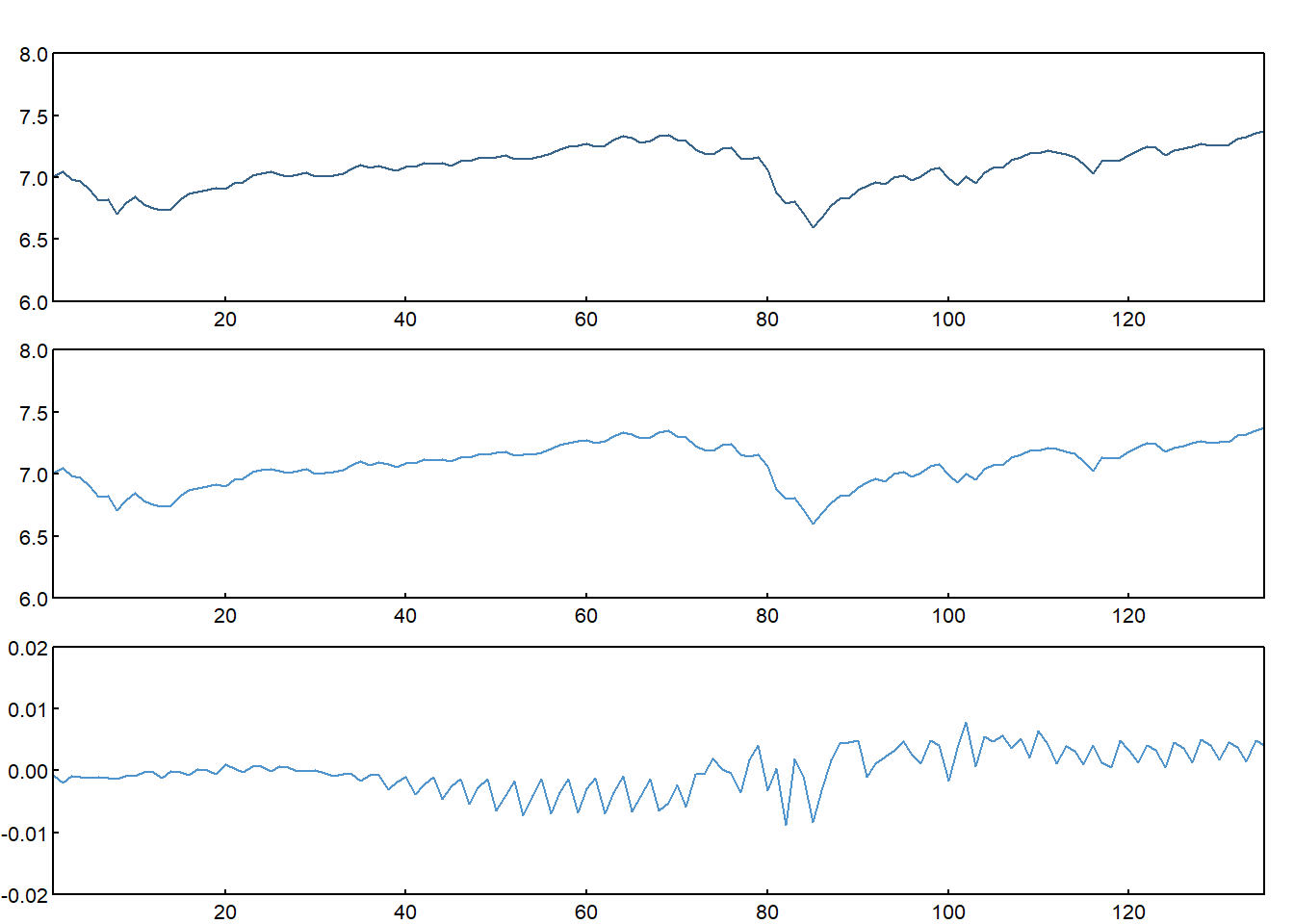
Screenshot 8.2 Actual, fitted and residual plot to check for stationarity (Page 401)
data = read.dta("Dataset/SandPhedge.dta")
lm1 = lm(lspot~lfutures,data=data)
summary(lm1)
##
## Call:
## lm(formula = lspot ~ lfutures, data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.0088008 -0.0014023 -0.0003198 0.0021394 0.0077902
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.025310 0.012061 2.099 0.0377 *
## lfutures 0.996468 0.001704 584.661 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.003362 on 133 degrees of freedom
## Multiple R-squared: 0.9996, Adjusted R-squared: 0.9996
## F-statistic: 3.418e+05 on 1 and 133 DF, p-value: < 2.2e-16
par(mfcol = c(3,1), oma = c(0,0,1,0) + 0.2, mar = c(0,1,0,0) + 1, mgp = c(0, 0.2, 0))
plot(data$lspot,type="l",las=1,xlab="",ylab="",main="",xaxs="i",yaxs="i",tck=.02,col="steelblue4",ylim=c(6,8))
plot(lm1$fitted.values,type="l",las=1,xlab="",ylab="",main="",xaxs="i",yaxs="i",tck=.02,col="steelblue3",ylim=c(6,8))
plot(lm1$residuals,type="l",las=1,xlab="",ylab="",main="",xaxs="i",yaxs="i",tck=.02,col="steelblue3",ylim=c(-0.02,0.02))
Testing for cointegration (Page 402)
df.res = ur.df(lm1$residuals,lags=2,type="drift")
df.res@testreg
##
## Call:
## lm(formula = z.diff ~ z.lag.1 + 1 + z.diff.lag)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.0109049 -0.0007591 -0.0001212 0.0007334 0.0089030
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 7.969e-05 1.934e-04 0.412 0.6810
## z.lag.1 -1.202e-01 6.913e-02 -1.738 0.0845 .
## z.diff.lag1 -6.589e-01 8.389e-02 -7.854 1.42e-12 ***
## z.diff.lag2 -5.582e-01 7.428e-02 -7.514 8.71e-12 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.002221 on 128 degrees of freedom
## Multiple R-squared: 0.5061, Adjusted R-squared: 0.4946
## F-statistic: 43.73 on 3 and 128 DF, p-value: < 2.2e-16
Cointegration Test (Page 406)
data = read.dta("Dataset/macro.dta")
df = data.frame(data$USTB10Y,data$USTB1Y,data$USTB3M,data$USTB3Y,data$USTB5Y,data$USTB6M)
p=3
jo.ci.trace = ca.jo(df,type="trace",ecdet="const",K=p+1)
summary(jo.ci.trace)
##
## ######################
## # Johansen-Procedure #
## ######################
##
## Test type: trace statistic , without linear trend and constant in cointegration
##
## Eigenvalues (lambda):
## [1] 1.373725e-01 1.185885e-01 8.964990e-02 4.634717e-02 2.483427e-02 7.987276e-03 8.153200e-17
##
## Values of teststatistic and critical values of test:
##
## test 10pct 5pct 1pct
## r <= 5 | 2.58 7.52 9.24 12.97
## r <= 4 | 10.68 17.85 19.96 24.60
## r <= 3 | 25.96 32.00 34.91 41.07
## r <= 2 | 56.20 49.65 53.12 60.16
## r <= 1 | 96.85 71.86 76.07 84.45
## r = 0 | 144.43 97.18 102.14 111.01
##
## Eigenvectors, normalised to first column:
## (These are the cointegration relations)
##
## data.USTB10Y.l4 data.USTB1Y.l4 data.USTB3M.l4 data.USTB3Y.l4 data.USTB5Y.l4
## data.USTB10Y.l4 1.0000000 1.000000 1.0000000 1.0000000 1.00000000
## data.USTB1Y.l4 -6.7348169 -5.852282 -2.9674724 0.9370732 -0.06084815
## data.USTB3M.l4 -4.5669473 0.751493 2.5491180 0.2850950 -0.06281291
## data.USTB3Y.l4 4.0561742 -17.238836 5.4836484 0.9824287 0.54586734
## data.USTB5Y.l4 -3.2821195 11.470920 -4.5162308 -2.1913592 -1.42474873
## data.USTB6M.l4 9.4830397 11.048983 -1.6063534 -0.9661132 0.06560961
## constant -0.4412386 -5.257480 0.4937381 -0.2650234 -0.69346419
## data.USTB6M.l4 constant
## data.USTB10Y.l4 1.00000000 1.00000000
## data.USTB1Y.l4 -0.09406147 0.37329716
## data.USTB3M.l4 -0.12530350 -0.58224116
## data.USTB3Y.l4 0.54989363 3.51288142
## data.USTB5Y.l4 -1.20164104 -4.71131952
## data.USTB6M.l4 0.18999602 -0.06925111
## constant -1.61396696 3.92524749
##
## Weights W:
## (This is the loading matrix)
##
## data.USTB10Y.l4 data.USTB1Y.l4 data.USTB3M.l4 data.USTB3Y.l4 data.USTB5Y.l4
## data.USTB10Y.d 0.05690502 -0.005886205 0.08166862 0.12974599 0.02429021
## data.USTB1Y.d 0.06011374 -0.013113342 0.03704386 0.04221975 0.12632957
## data.USTB3M.d 0.08534176 -0.021186294 -0.02974528 0.04163139 0.08187311
## data.USTB3Y.d 0.04302183 -0.005157639 0.03880503 0.13379182 0.11657737
## data.USTB5Y.d 0.05752479 -0.004287452 0.07114089 0.16726624 0.08141523
## data.USTB6M.d 0.03958347 -0.020450550 0.01672614 0.04243206 0.10327850
## data.USTB6M.l4 constant
## data.USTB10Y.d -0.028240500 1.074784e-15
## data.USTB1Y.d -0.017173146 -2.794624e-15
## data.USTB3M.d -0.007619134 -3.291100e-15
## data.USTB3Y.d -0.027423330 1.036733e-15
## data.USTB5Y.d -0.026315900 1.840829e-15
## data.USTB6M.d -0.011131403 -1.856540e-15
Johansen System Cointegration Test (Page 407)
jo.ci.eigen = ca.jo(df,type="trace",ecdet="const",K=p+1)
summary(jo.ci.eigen)
##
## ######################
## # Johansen-Procedure #
## ######################
##
## Test type: trace statistic , without linear trend and constant in cointegration
##
## Eigenvalues (lambda):
## [1] 1.373725e-01 1.185885e-01 8.964990e-02 4.634717e-02 2.483427e-02 7.987276e-03 8.153200e-17
##
## Values of teststatistic and critical values of test:
##
## test 10pct 5pct 1pct
## r <= 5 | 2.58 7.52 9.24 12.97
## r <= 4 | 10.68 17.85 19.96 24.60
## r <= 3 | 25.96 32.00 34.91 41.07
## r <= 2 | 56.20 49.65 53.12 60.16
## r <= 1 | 96.85 71.86 76.07 84.45
## r = 0 | 144.43 97.18 102.14 111.01
##
## Eigenvectors, normalised to first column:
## (These are the cointegration relations)
##
## data.USTB10Y.l4 data.USTB1Y.l4 data.USTB3M.l4 data.USTB3Y.l4 data.USTB5Y.l4
## data.USTB10Y.l4 1.0000000 1.000000 1.0000000 1.0000000 1.00000000
## data.USTB1Y.l4 -6.7348169 -5.852282 -2.9674724 0.9370732 -0.06084815
## data.USTB3M.l4 -4.5669473 0.751493 2.5491180 0.2850950 -0.06281291
## data.USTB3Y.l4 4.0561742 -17.238836 5.4836484 0.9824287 0.54586734
## data.USTB5Y.l4 -3.2821195 11.470920 -4.5162308 -2.1913592 -1.42474873
## data.USTB6M.l4 9.4830397 11.048983 -1.6063534 -0.9661132 0.06560961
## constant -0.4412386 -5.257480 0.4937381 -0.2650234 -0.69346419
## data.USTB6M.l4 constant
## data.USTB10Y.l4 1.00000000 1.00000000
## data.USTB1Y.l4 -0.09406147 0.37329716
## data.USTB3M.l4 -0.12530350 -0.58224116
## data.USTB3Y.l4 0.54989363 3.51288142
## data.USTB5Y.l4 -1.20164104 -4.71131952
## data.USTB6M.l4 0.18999602 -0.06925111
## constant -1.61396696 3.92524749
##
## Weights W:
## (This is the loading matrix)
##
## data.USTB10Y.l4 data.USTB1Y.l4 data.USTB3M.l4 data.USTB3Y.l4 data.USTB5Y.l4
## data.USTB10Y.d 0.05690502 -0.005886205 0.08166862 0.12974599 0.02429021
## data.USTB1Y.d 0.06011374 -0.013113342 0.03704386 0.04221975 0.12632957
## data.USTB3M.d 0.08534176 -0.021186294 -0.02974528 0.04163139 0.08187311
## data.USTB3Y.d 0.04302183 -0.005157639 0.03880503 0.13379182 0.11657737
## data.USTB5Y.d 0.05752479 -0.004287452 0.07114089 0.16726624 0.08141523
## data.USTB6M.d 0.03958347 -0.020450550 0.01672614 0.04243206 0.10327850
## data.USTB6M.l4 constant
## data.USTB10Y.d -0.028240500 1.074784e-15
## data.USTB1Y.d -0.017173146 -2.794624e-15
## data.USTB3M.d -0.007619134 -3.291100e-15
## data.USTB3Y.d -0.027423330 1.036733e-15
## data.USTB5Y.d -0.026315900 1.840829e-15
## data.USTB6M.d -0.011131403 -1.856540e-15
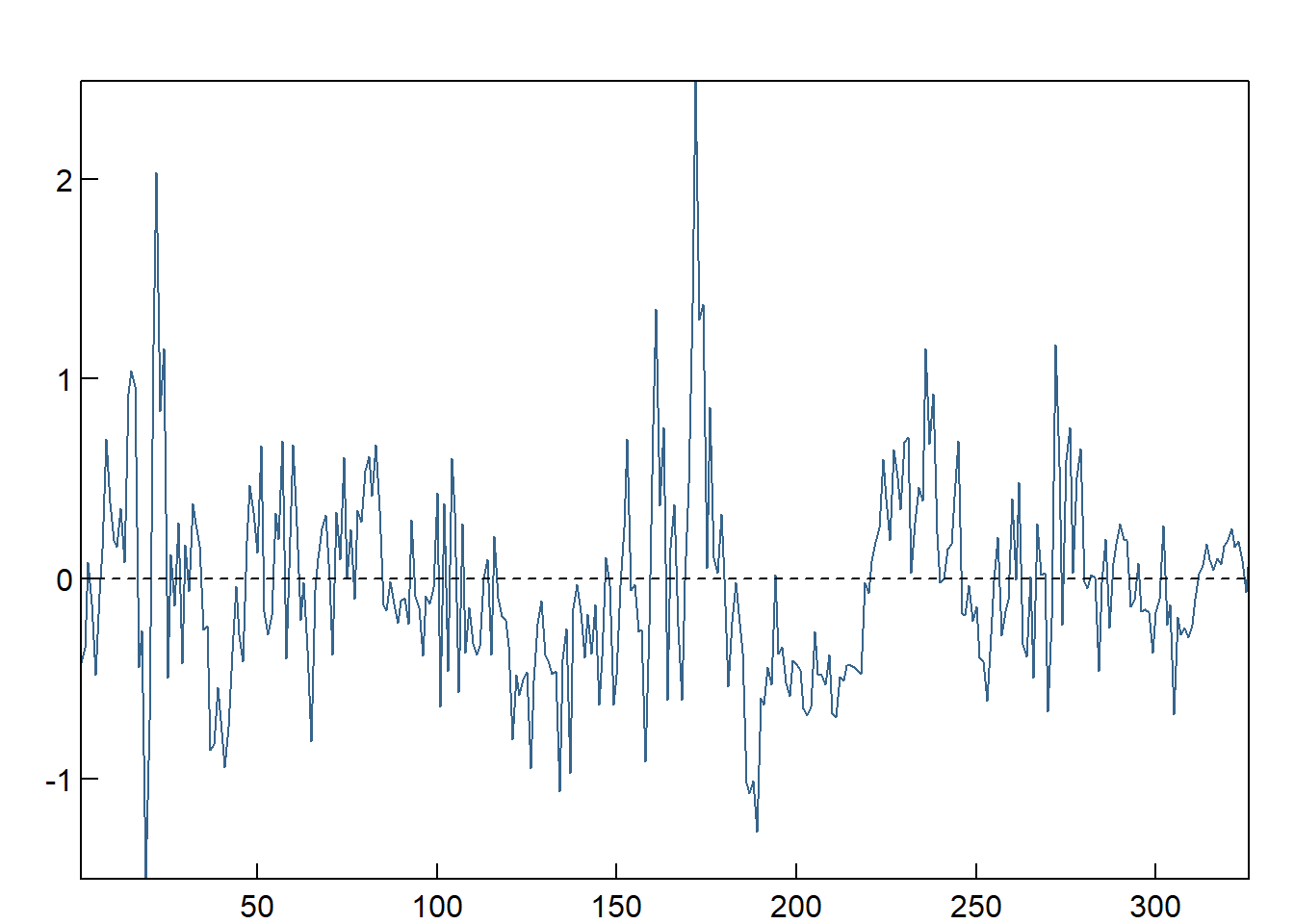
ECM = cbind(as.matrix(df),1)%*%jo.ci.eigen@V[,1]
par(mfcol = c(1,1), oma = c(0,0,1,0) + 0.2, mar = c(0,1,0,0) + 1, mgp = c(0, 0.2, 0))
plot(ECM,type="l",las=1,xlab="",ylab="",main="",xaxs="i",yaxs="i",tck=.02,col="steelblue4")
abline(h=0,lty=2)