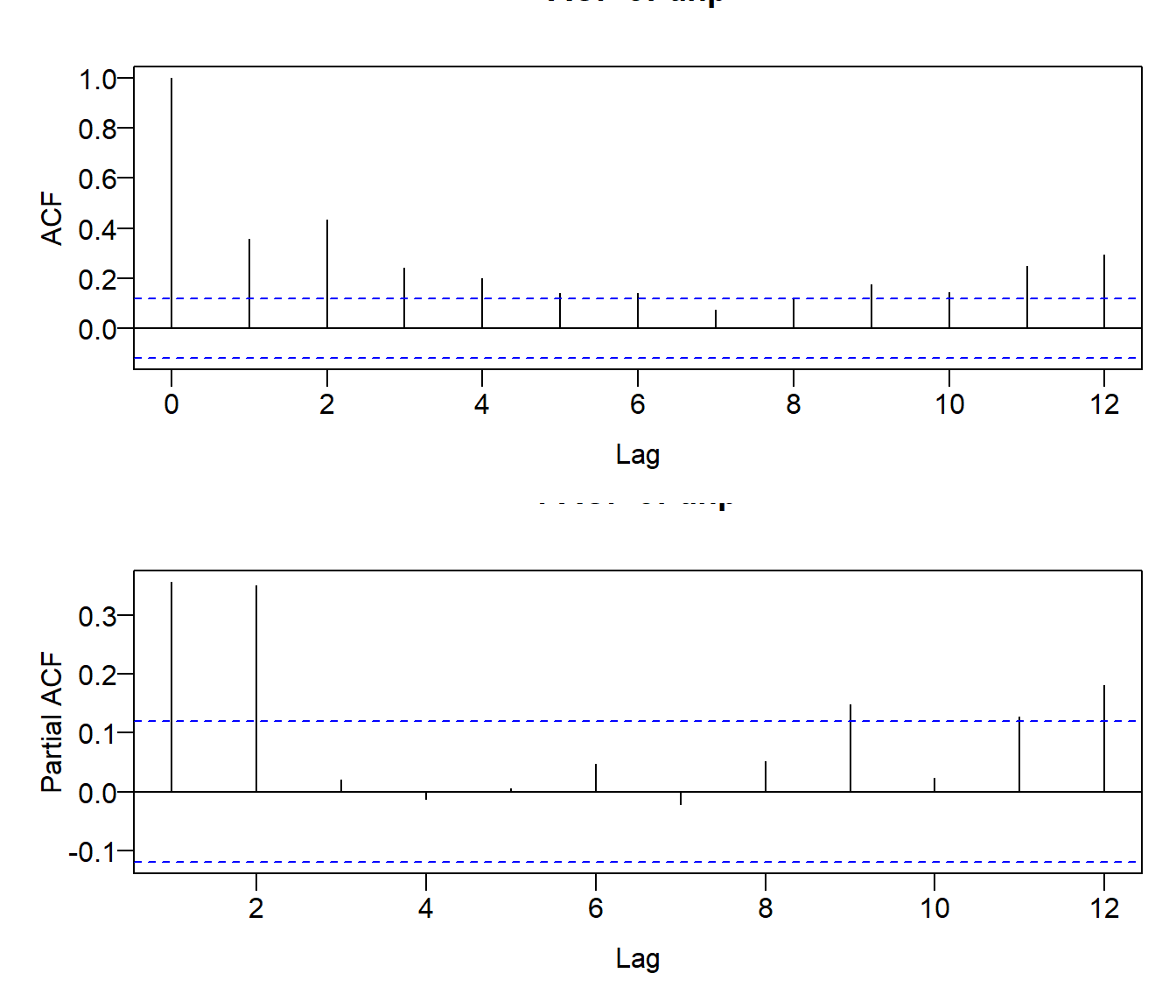
Screenshot 6.1 Estimating the correlogram (Page 277)
data_ukhp <- read.dta("Dataset/ukhp.dta")
data_ukhp <- na.omit(data_ukhp)
par(mfcol = c(2, 1), mar = c(4, 4, 2, 1), mgp = c(2, 0.5, 0))
acf(data_ukhp$dhp, lag = 12, las = 1, main = "ACF of dhp")
pacf(data_ukhp$dhp, lag = 12, las = 1, main = "PACF of dhp")
ARIMA (Page 279)
library(forecast)
summary(model <- Arima(data_ukhp$dhp, order = c(1, 0, 1), include.mean = TRUE))
## Series: data_ukhp$dhp
## ARIMA(1,0,1) with non-zero mean
##
## Coefficients:
## ar1 ma1 mean
## 0.8364 -0.5608 0.4441
## s.e. 0.0622 0.0941 0.1727
##
## sigma^2 = 1.154: log likelihood = -398.14
## AIC=804.29 AICc=804.44 BIC=818.65
##
## Training set error measures:
## ME RMSE MAE MPE MAPE MASE ACF1
## Training set 0.0001903891 1.068324 0.8169962 113.6997 205.435 0.8054493 -0.06479526
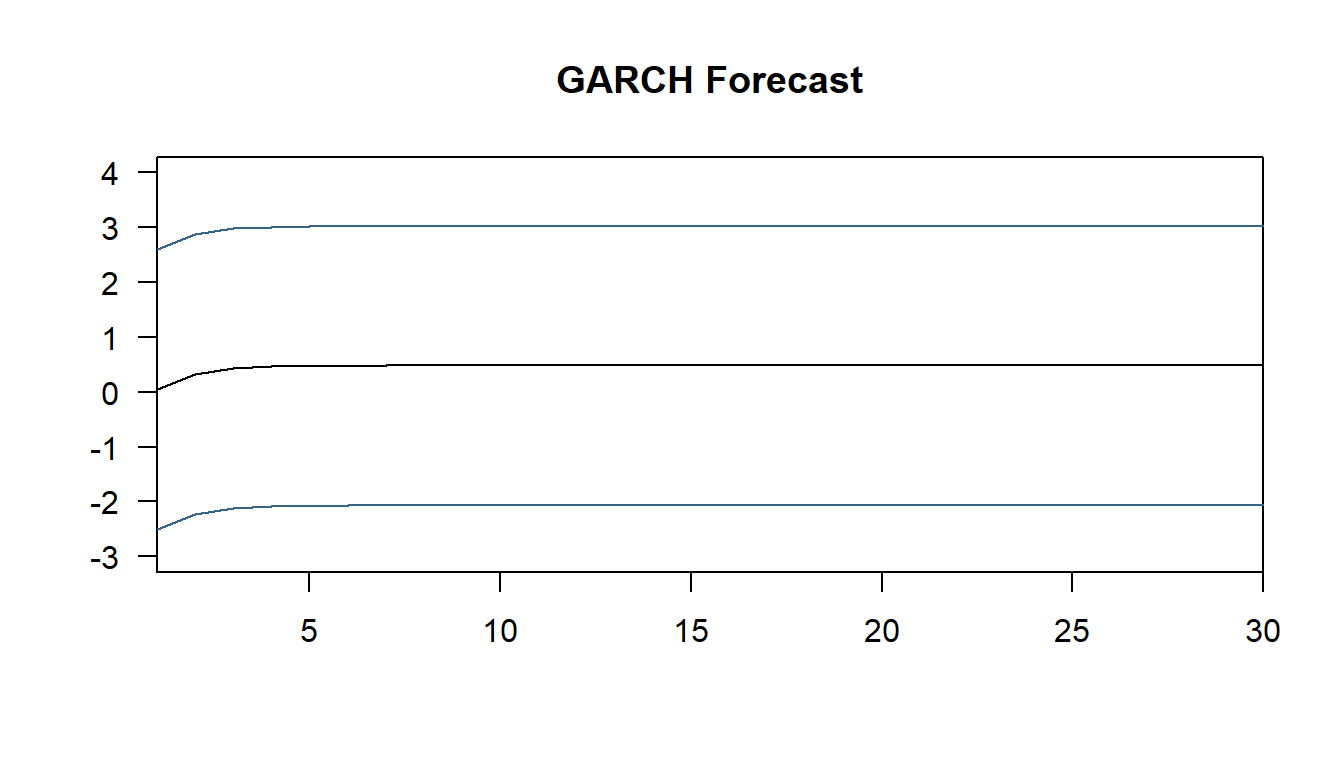
Screenshot 6.3 Dynamic forecasts for the percentage changes in house prices (Page 298)
space <- 30
nfore <- 30
ar2.spec <- ugarchspec(mean.model = list(armaOrder = c(1,0)),
variance.model = list(garchOrder = c(0,1)))
ar.fit <- ugarchfit(ar2.spec, data_ukhp$dhp[1:(nrow(data_ukhp)-space)])
ar.fore <- ugarchforecast(ar.fit, n.ahead = nfore)
c.mean <- ar.fore@forecast$seriesFor
c.lower <- c.mean - qnorm(0.99) * ar.fore@forecast$sigmaFor
c.upper <- c.mean + qnorm(0.99) * ar.fore@forecast$sigmaFor
plot(c.mean, type = "l", xaxs = "i", las = 1, main = "GARCH Forecast",
ylim = c(-3, 4), ylab = "", xlab = "")
lines(c.lower, col = "steelblue4")
lines(c.upper, col = "steelblue4")
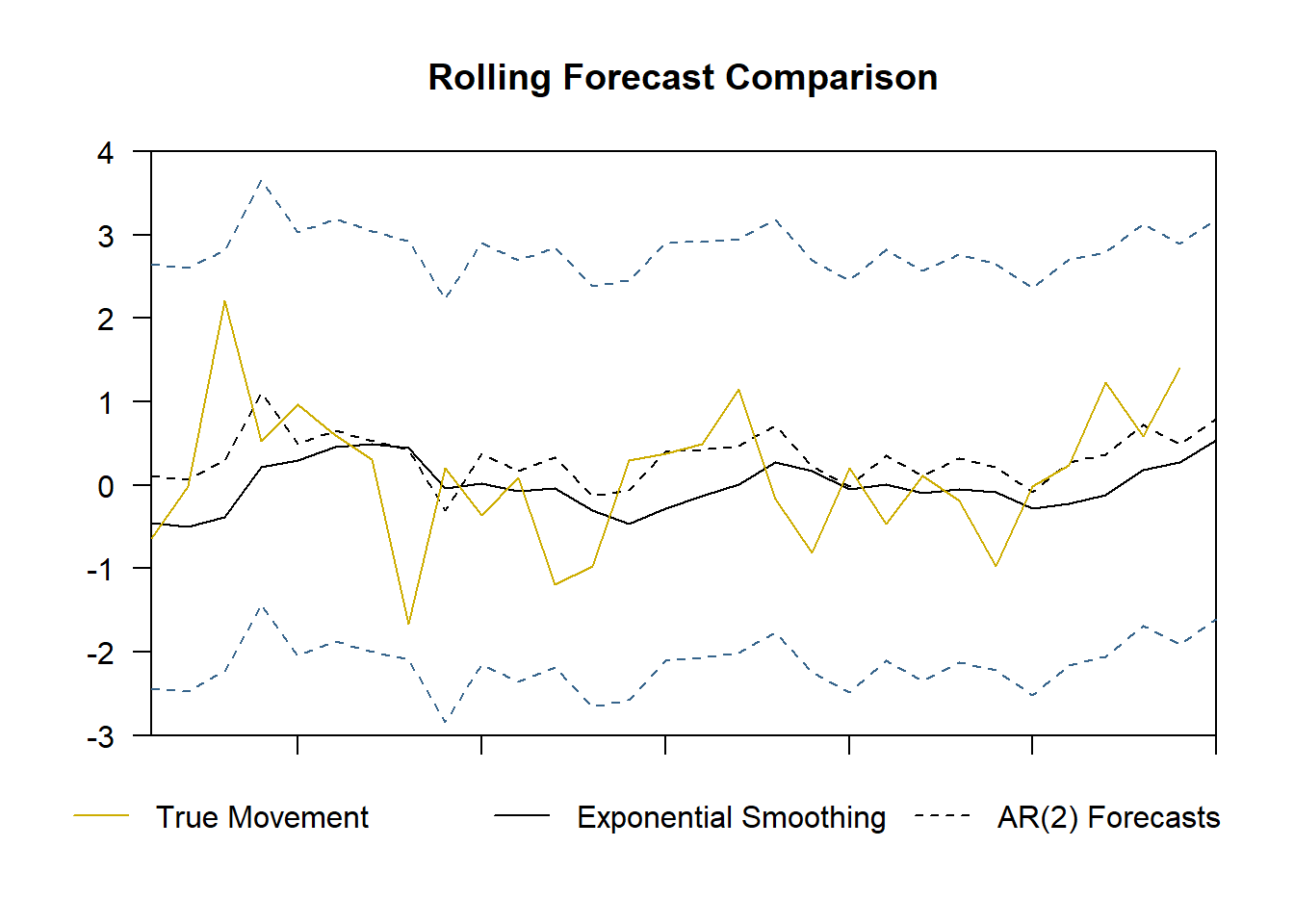
Screenshot 6.4 Static forecasts for the percentage changes in house prices (Page 298)
FORE.EX <- FORE.AR2 <- NULL
for (i in 1:space) {
ar.fit <- ugarchfit(ar2.spec, data_ukhp$dhp[1:(nrow(data_ukhp)-space+i)])
ar.fore <- ugarchforecast(ar.fit, n.ahead = 1)
c.mean <- ar.fore@forecast$seriesFor
c.lower <- c.mean - qnorm(0.99) * ar.fore@forecast$sigmaFor
c.upper <- c.mean + qnorm(0.99) * ar.fore@forecast$sigmaFor
FORE.AR2 <- rbind(FORE.AR2, c(c.mean, c.lower, c.upper))
es.fore <- es(data_ukhp$dhp[1:(nrow(data_ukhp)-space+i)], h = 1, holdout = FALSE, silent = TRUE, intervals = "parametric")
FORE.EX <- rbind(FORE.EX, c(es.fore$forecast, es.fore$lower, es.fore$upper))
}
plot(FORE.EX[,1], type = "l", xaxs = "i", yaxs = "i", las = 1, ylim = c(-3, 4),
main = "Rolling Forecast Comparison", ylab = "", xlab = "")
#lines(FORE.EX[,2], col = "steelblue4")
#lines(FORE.EX[,3], col = "steelblue4")
lines(FORE.AR2[,1], lty = 2)
lines(FORE.AR2[,2], col = "steelblue4", lty = 2)
lines(FORE.AR2[,3], col = "steelblue4", lty = 2)
lines(data_ukhp$dhp[-(1:(nrow(data_ukhp)-space+1))], col = "gold3", lwd = 1)
legend("bottom",
legend = c("True Movement", "Exponential Smoothing", "AR(2) Forecasts"),
col = c("gold3", "black", "black"),
lty = c(1, 1, 2),
box.col = "white",
xpd = TRUE,
inset = c(0, -0.2),
ncol = 3)